Satz von Lindemann-Weierstrass
- Satz von Lindemann-Weierstrass
-
Der Satz von Lindemann-Weierstraß ist ein zahlentheoretisches Ergebnis über die Nichtexistenz von Nullstellen bei gewissen Exponentialpolynomen, woraus dann beispielsweise die Transzendenz von e und π folgt. Er ist benannt nach den beiden Mathematikern Carl Louis Ferdinand von Lindemann und Karl Weierstraß. In exakter Form lautet er: Sind α1,...,αn paarweise verschiedene algebraische Zahlen und β1,...,βn beliebige algebraische Zahlen, wobei nicht alle βk = 0 sind, dann gilt
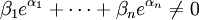 .
.
Diesen sehr allgemeinen Satz bewies von Lindemann, um die deutlich schwächeren Resultate der Transzendenz von e und π zu zeigen.
Folgerungen
Diese Ergebnisse folgen tatsächlich direkt aus dem obigen Theorem:
Wäre e eine algebraische Zahl, so existierten β0,...,βn, nicht allesamt null, so dass
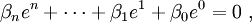
was ein offensichtlicher Widerspruch zum obigen Ergebnis wäre.
Um die Transzendenz der Kreiszahl π zu zeigen, gehen wir auch hier zunächst davon aus, dass π eine algebraische Zahl sei. Weil die Menge der algebraischen Zahlen einen Körper bilden, müsste auch πi algebraisch sein (für i siehe imaginäre Einheit).
Wenn wir nun β1 = β2 = 1 und α1 = πi, α2 = 0 wählen, erhalten wir mit dem Satz von Lindemann-Weierstraß den Widerspruch
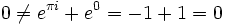 (siehe auch: eulersche Identität),
(siehe auch: eulersche Identität),
und dies zeigt, dass unsere Annahme falsch war, also dass π transzendent sein muss.
Kurze Zeit nach dem Beweis des Satzes von Lindemann-Weierstraß legte David Hilbert einen deutlich vereinfachten Beweis für die Spezialfälle der Transzendenz der Zahlen e und π vor, aus dem sich wiederum auch der allgemeine Satz folgern lässt. Dieser Beweis findet sich unter den Weblinks.
Literatur
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Weierstrass — Karl Weierstraß Karl Theodor Wilhelm Weierstraß (* 31. Oktober 1815 in Ostenfelde bei Ennigerloh/Münsterland; † 19. Februar 1897 in Berlin) war ein deutscher Mathematiker, der sich vor allem um die logisch fundierte Aufarbeitung der Analysis… … Deutsch Wikipedia
Vermutung von Schanuel — Die Vermutung von Schanuel ist eine bis heute unbewiesene mathematische Aussage über die Transzendenzgrade von bestimmten Körpererweiterungen des Körpers der rationalen Zahlen. Diese Vermutung gehört also in den Bereich der… … Deutsch Wikipedia
Karl Weierstrass — Karl Weierstraß Karl Theodor Wilhelm Weierstraß (* 31. Oktober 1815 in Ostenfelde bei Ennigerloh/Münsterland; † 19. Februar 1897 in Berlin) war ein deutscher Mathematiker, der sich vor allem um die logisch fundierte Aufarbeitung der Analysis… … Deutsch Wikipedia
Karl Theodor Weierstraß — Karl Weierstraß Karl Theodor Wilhelm Weierstraß (* 31. Oktober 1815 in Ostenfelde bei Ennigerloh/Münsterland; † 19. Februar 1897 in Berlin) war ein deutscher Mathematiker, der sich vor allem um die logisch fundierte Aufarbeitung der Analysis… … Deutsch Wikipedia
Karl Theodor Wilhelm Weierstraß — Karl Weierstraß Karl Theodor Wilhelm Weierstraß (* 31. Oktober 1815 in Ostenfelde bei Ennigerloh/Münsterland; † 19. Februar 1897 in Berlin) war ein deutscher Mathematiker, der sich vor allem um die logisch fundierte Aufarbeitung der Analysis… … Deutsch Wikipedia
Weierstraß — Karl Weierstraß Karl Theodor Wilhelm Weierstraß (* 31. Oktober 1815 in Ostenfelde bei Ennigerloh/Münsterland; † 19. Februar 1897 in Berlin) war ein deutscher Mathematiker, der sich vor allem um die logisch fundierte Aufarbeitung der Analysis… … Deutsch Wikipedia
Karl Weierstraß — ist auf der Ehrentafel ehemaliger Schüler d … Deutsch Wikipedia
Liste mathematischer Sätze — Inhaltsverzeichnis A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A Satz von Abel Ruffini: eine allgemeine Polynomgleichung vom … Deutsch Wikipedia
Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
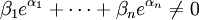 .
.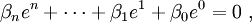
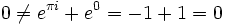 (siehe auch: eulersche Identität),
(siehe auch: eulersche Identität),