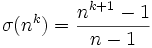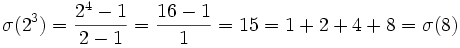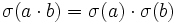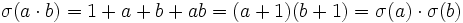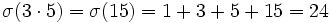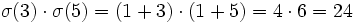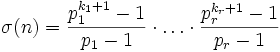Satz von Thabit

Unter der Teilersumme σ einer natürlichen Zahl versteht man die Summe aller Teiler dieser Zahl einschließlich der Zahl selbst.

Beispiel:

Die Zahl 6 hat die Teiler 1, 2, 3 und 6. Die Teilersumme für 6 lautet also 1+2+3+6 = 12.

Bei vielen Problemstellungen der Zahlentheorie spielen Teilersummen eine Rolle, z. B. bei den vollkommenen Zahlen und den befreundeten Zahlen.

Definitionen

Definition 1: Summe aller Teiler

Seien t₁,t₂,...,t_k alle Teiler der natürlichen Zahl n, dann nennt man σ(n) = t₁ + t₂ + ... + t_k die Teilersumme von n. Dabei sind 1 und n selbst Teiler, also in der Menge der Teiler enthalten. Die Funktion σ heißt Teilersummenfunktion und ist eine zahlentheoretische Funktion.

Das Beispiel oben kann man nun so schreiben:

σ(6) = 1 + 2 + 3 + 6 = 12

Definition 2: Summe der echten Teiler

Die Summe der echten Teiler der natürlichen Zahl n ist die Summe der Teiler von n ohne die Zahl n selbst und wir bezeichnen diese Summe mit σ ^* (n).

Beispiel:

σ ^* (6) = 1 + 2 + 3 = 6

Offensichtlich gilt die Beziehung:

σ(n) − n = σ ^* (n)

Definition 3: defizient, abundant, vollkommen

Eine natürliche Zahl n > 1 heißt

defizient oder teilerarm, wenn σ ^* (n) < n,

abundant oder teilerreich, wenn σ ^* (n) > n,

vollkommen, wenn σ ^* (n) = n.

Beispiele:

σ ^* (6) = 1 + 2 + 3 = 6, d. h. 6 ist eine vollkommene Zahl.

σ ^* (12) = 1 + 2 + 3 + 4 + 6 = 16 > 12, d. h. 12 ist abundant.

σ ^* (10) = 1 + 2 + 5 = 8 < 10, d. h. 10 ist defizient.

Eigenschaften der Teilersumme

Satz 1: Teilersumme einer Primzahl

Sei n eine Primzahl. Dann gilt:

σ(n) = n + 1

Beweis: Da n eine Primzahl ist, sind 1 und n die einzigen Teiler. Daraus folgt die Behauptung.

Satz 2: Teilersumme der Potenz einer Primzahl

Sei n eine Primzahl. Dann gilt:

$\sigma(n^k) = \frac{n^{k+1}-1}{n-1}$

Beweis: Da n eine Primzahl ist, lauten die Teiler von n^k: n⁰, n¹, …, n^k. Die Summe ist eine geometrische Reihe. Aus der Summenformel für eine geometrische Reihe folgt sofort die Behauptung.

Beispiel:

$\sigma(2^3) = {{2^4-1} \over {2-1}} = {{16-1} \over 1} = 15 = 1+2+4+8 = \sigma(8)$

Satz 3: Teilersumme des Produktes von zwei Primzahlen

Seien a und b verschiedene Primzahlen. Dann gilt:

$\sigma(a\cdot b) = \sigma(a) \cdot \sigma(b)$

Beweis: Die Zahl ab besitzt die vier verschiedenen Teiler 1, a, b und ab. Daraus folgt:

$\sigma(a \cdot b) = 1 + a + b + ab = (a+1)(b+1) = \sigma(a) \cdot \sigma(b)$

Beispiel:

$\sigma(3 \cdot 5) = \sigma(15) = 1+3+5+15 = 24$

$\sigma(3) \cdot \sigma(5) = (1+3) \cdot (1+5) = 4 \cdot 6 = 24$

Satz 4: Verallgemeinerung von Satz 3

Seien p₁,p₂,...,p_r Primzahlen und k₁,k₂,...,k_r natürliche Zahlen. Ferner sei 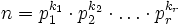$n = p_1^{k_1} \cdot p_2^{k_2} \cdot\ldots\cdot p_r^{k_r}$. Dann gilt:

$\sigma(n) = \frac{p_1^{k_1+1}-1}{p_1-1} \cdot\ldots\cdot \frac{p_r^{k_r+1}-1}{p_r-1}$

Satz von Thabit

Mit Hilfe von Satz 4 kann man den Satz von Thabit aus dem Gebiet der befreundeten Zahlen beweisen. Der Satz lautet:

Für eine feste natürliche Zahl n seien x = 3·2ⁿ-1, y = 3·2^n-1-1 und z = 9·2^2n-1-1.

Wenn x, y und z Primzahlen größer als 2 sind, dann sind die beiden Zahlen a = 2ⁿ·x·y und b = 2ⁿ·z befreundet, d. h. σ ^* (a) = b und σ ^* (b) = a.

Beweis:

σ^*(a) = σ(a) - a

= σ(2ⁿ·x·y) - a

= (2ⁿ⁺¹-1)(x+1)(y+1) - a (Satz 4)

= (2ⁿ⁺¹-1)(3·2ⁿ)(3·2^n-1) - 2ⁿ(3·2ⁿ-1)(3·2^n-1-1)

= (2ⁿ⁺¹-1)·9·2^2n-1 - 2ⁿ(9·2^2n-1-6·2^n-1-3·2^n-1+1)

= 2·2ⁿ·9·2^2n-1-9·2ⁿ·2^n-1-2ⁿ(9·2^2n-1-9·2^n-1+1)

= 2ⁿ(18·2^2n-1-9·2^n-1-9·2^2n-1+9·2^n-1-1)

= 2ⁿ(9·2^2n-1-1)

= 2ⁿ·z

= b

Analog zeigt man σ ^* (b) = a.

Teilersumme als endliche Reihe

Für jede natürliche Zahl n kann die Teilerfunktion als Reihe dargestellt werden, ohne dass auf die Teilbarkeitseigenschaften von n explizit Bezug genommen wird:

$\sigma(n) =\sum_{\mu=1}^n\sum_{\nu=1}^\mu \cos{2\pi\frac{\nu n}{\mu}}$

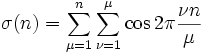
Beweis: Die Funktion

$T(n,\mu) = \frac{1}{\mu}\sum_{\nu=1}^\mu\cos 2\pi \frac{\nu n}{\mu},\quad n=1,2,\dots, \quad \mu=1,2,\dots$

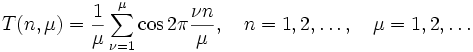
wird 1, wenn μ ein Teiler von n ist, ansonsten bleibt sie Null. Zunächst gilt

$T(n,\mu) = \frac{1}{\mu}\lim_{x \to n} \sum_{\nu=1}^\mu\cos 2\pi \frac{\nu x}{\mu} = \lim_{x \to n} \frac{1}{2\mu}\left(\sin 2\pi x \cot\frac{\pi x}{\mu} - 1 +\cos 2\pi x\right) = \lim_{x \to n} \frac{\sin 2\pi x \cos\frac{\pi x}{\mu}}{2\mu\sin\frac{\pi x}{\mu}}$

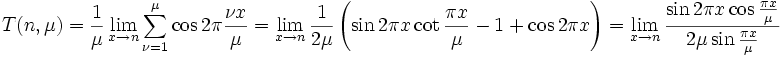
Der Zähler im letzten Ausdruck wird stets Null, wenn 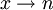$x\to n$ geht. Der Nenner kann nur dann Null werden, wenn μ ein Teiler von n ist. Dann ist aber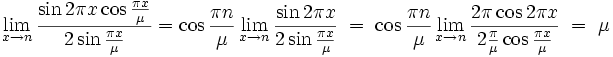

$\lim_{x \to n} \frac{\sin 2\pi x \cos\frac{\pi x}{\mu}}{2\sin\frac{\pi x}{\mu}} = \cos\frac{\pi n}{\mu} \lim_{x \to n} \frac{\sin 2\pi x }{2\sin\frac{\pi x}{\mu}} \;=\; \cos\frac{\pi n}{\mu} \lim_{x \to n} \frac{2\pi \cos 2\pi x }{2\frac{\pi}{\mu}\cos\frac{\pi x}{\mu}} \;=\; \mu$

Nur in diesem Fall wird T(n,μ) = 1, wie oben behauptet.

Multipliziert man jetzt T(n,μ) mit μ^k und summiert das Produkt über alle Werte μ = 1 bis μ = n, so entsteht nur dann ein Beitrag μ^k zur Summe, wenn μ ein Teiler von n ist. Das ist aber genau die Definition der allgemeinen Divisorfunktion

$\sigma_k(n) =\sum_{\mu=1}^n\mu^{k-1}\sum_{\nu=1}^\mu \cos{2\pi\frac{\nu n}{\mu}},\quad k=0,\pm 1,\dots$

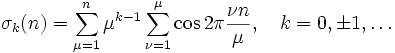
deren Spezialfall k = 1 die einfache Teilersumme σ(n) ist.

Siehe auch

• Teilermenge