Satz von Tichonow

Der Satz von Tichonow (nach Andrei Nikolajewitsch Tichonow) ist eine Aussage aus dem mathematischen Teilgebiet der Topologie. Er lautet:

Ist 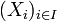$(X_i)_{i \in I}$ eine Familie kompakter topologischer Räume, dann ist auch das kartesische Produkt 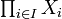$\textstyle \prod_{i\in I} X_{i}$ mit der Produkttopologie kompakt.

Diskussion

Der Satz scheint auf den ersten Blick der Anschauung zu widersprechen. Kompaktheit ist in gewisser Weise eine Endlichkeitseigenschaft (jede offene Überdeckung hat eine endliche Teilüberdeckung), und es mag verwundern, dass sich dies auf ein Produkt mit beliebig vielen Faktoren überträgt. Man denke dabei etwa an das Lemma von Riesz aus der Funktionalanalysis, wonach die abgeschlossene Einheitskugel eines normierten Raumes nur in endlichdimensionalen Räumen kompakt ist, oder auch daran, dass eine beliebige Vereinigung kompakter Mengen im Allgemeinen nicht mehr kompakt ist. Was die Anschauung hier in die Irre führt, ist der Begriff der Umgebung, des „in der Nähe von“ in der Produkttopologie. Denn wenn ein Punkt 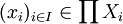$(x_i)_{i \in I} \in \prod X_{i}$ in der Nähe von 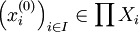$\left(x_i^{(0)}\right)_{i \in I} \in \prod X_{i}$ liegt, bedeutet das in der Produkttopologie eben nur, dass es endliche viele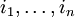 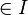$i_1,\ldots,i_n$ $\in I$ gibt, so dass 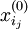$x^{(0)}_{i_j}$ in der Nähe von 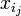$x_{i_j}$ liegt für $j=1,\ldots,n$.

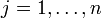Der Beweis nutzt das Lemma von Zorn. Tatsächlich ist der Satz von Tichonow sogar äquivalent zu dem Lemma von Zorn.

Literatur

• Jänich: Topologie. Springer-Verlag, Berlin, 1994, S.197 ff.
• Skript zur Mengentheoretische Topologie (im PDF-Format, deutsch)