- Satz von Tschebyscheff
-
Ein binomisches Integral ist ein Integral der Form:
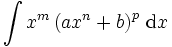 , wobei
, wobei 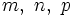 rationale Zahlen sind und
rationale Zahlen sind und 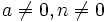 .
.Mit dem binomischen Integral und nach dem Satz von Tschebyscheff kann man bestimmen, ob eine Funktion elementar integrierbar ist, oder nicht.
Satz von Tschebyscheff:
Ein Binomisches Integral ist elementar integrierbar genau dann, wenn mindestens eine der rationalen Zahlen
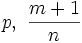 bzw.
bzw. 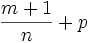 ganz ist.
ganz ist.Beispiel 1:
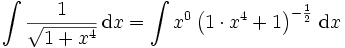
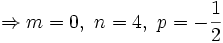
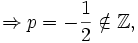
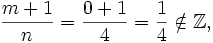
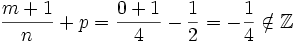
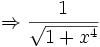 ist nicht elementar integrierbar
ist nicht elementar integrierbarBeispiel 2:
![\int \sqrt[3]{x} \sqrt[3]{ \left(x+1 \right)^2} \,\mathrm{d}x = \int x^{ \frac{1}{3}} \left(1 \cdot x^1 +1 \right)^{ \frac{2}{3}} \,\mathrm{d}x](/pictures/dewiki/51/37e0f8c1ef4129833596d370f44241fb.png)
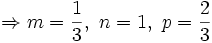
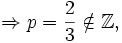
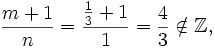
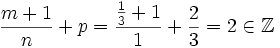
![\Rightarrow \sqrt[3]{x} \sqrt[3]{ \left(x+1 \right)^2}](/pictures/dewiki/55/7838c0dc86839e573fa22fe98b3a31c5.png) ist elementar integrierbar
ist elementar integrierbarAuffinden der Stammfunktion:
Ist die Funktion elementar integrierbar, so läßt sich mitfolgenden Substitutionen eine explizite Stammfunktion finden:
p ganz: x = tq wobei q der Hauptnenner von m und n ist
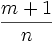 ganz: tq = axn + b wobei q der Nenner von p ist
ganz: tq = axn + b wobei q der Nenner von p ist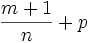 ganz:
ganz: 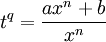 wobei q der Nenner von p ist
wobei q der Nenner von p ist
Wikimedia Foundation.
