- Schallspektrum
-
Ein Schallspektrum (auch: akustisches Spektrum) ist die grafische Darstellung des Ergebnisses der Zerlegung eines akustischen Signals (Schallvorgang) in die den einzelnen Teilfrequenzen zuzuordnenden Anteile. Es handelt sich somit um ein Frequenzspektrum, anhand dessen die Verteilung von Schalldrücken, Schallintensitäten oder Schallleistungen (Amplituden) beziehungsweise deren Pegelwerten (Amplitudenspektrum) ausgewertet werden kann.
Es wird unterschieden zwischen sogenannten Schmalbandspektren und Breitbandspektren. Bei Schmalbandspektren werden die Messgrößen in festen Frequenzbändern mit konstanter Breite angegeben, bei Breitbandspektren werden Oktavbänder („Oktavspektrum“) oder Unterteilungen von Oktavbändern wie z. B. Terzen („Terzspektrum“, „1/3-Oktavspektrum“) genutzt.
Ein kontinuierliches Spektrum ist ein Spektrum eines Schallvorgangs, das alle Frequenzen im gesamten Hörbereich oder in Teilabschnitten dieses Bereichs enthält, im Gegensatz zum Linienspektrum, das sich aus einer Reihe von Einzelfrequenzen - wie bei musikalischen Klängen - zusammensetzt.
Ein solches akustisches Spektrum wird in aller Regel in einem rechtwinkligen Koordinatensystem dargestellt, wobei auf der Abszisse die Frequenz meistens logarithmisch abgetragen wird und auf der Ordinate eine frequenzabhängige Größe, z. B. der Schalldruck, dargestellt wird.
Das Spektrum einer periodischen Funktion in ihre Komponenten kann mathematisch, beispielsweise durch Fourier-Analyse, errechnet werden, wobei man deren Amplituden und Phasen erhält, die in Amplituden- oder Phasenspektren dargestellt werden können. Meistens ist die Kenntnis eines Amplitudenspektrums ausreichend. Eine Zusammenfassung von Amplitudenspektrum und Phasenspektrum nennt man komplexes Amplitudenspektrum. Wird auf der Ordinate der Pegel dargestellt, so spricht man von einem Pegelspektrum. Eine solche Pegeldarstellung ist z. B. zweckmäßig, wenn auch schwache Komponenten dargestellt werden sollen.
Beim gemessenen Spektrum erfolgt die messtechnische Zerlegung über elektrische Filter. Dabei ergeben Filter mit konstanter Absolutbandbreite bei der Messung nach dem Suchtonverfahren eine kontinuierliche Analyse, wobei die angemessene Darstellungsart das Pegel-Frequenzspektrum ist. Bei Verwendung von Filtern mit konstanter Relativbandbreite erhält man bei Verwendung von Oktavfiltern sogenannte Oktavpegeldiagramme (Grobanalyse) und bei Verwendung von Terzfiltern sogenannte Terzpegeldiagramme (Feinanalyse).
Ein typisches Beispiel für einen Schallvorgang mit kontinuierlichem Spektrum ist „Weißes Rauschen“, das alle Frequenzen im gesamten Hörbereich im zeitlichen Mittel mit gleicher Stärke enthält. Wird solches weißes Rauschen über ein Terzfilter geschickt, so ergibt sich ein Rauschen mit kontinuierlichem Spektrum, das im Wesentlichen nur die Frequenzen im Bereich einer Terz enthält. Solche Rauschvorgänge werden in der akustischen Messtechnik häufig als Mess-Signale verwendet.
Beispiel
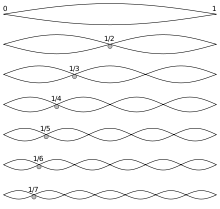 Harmonische Obertöne einer idealisierten Saite
Harmonische Obertöne einer idealisierten Saite
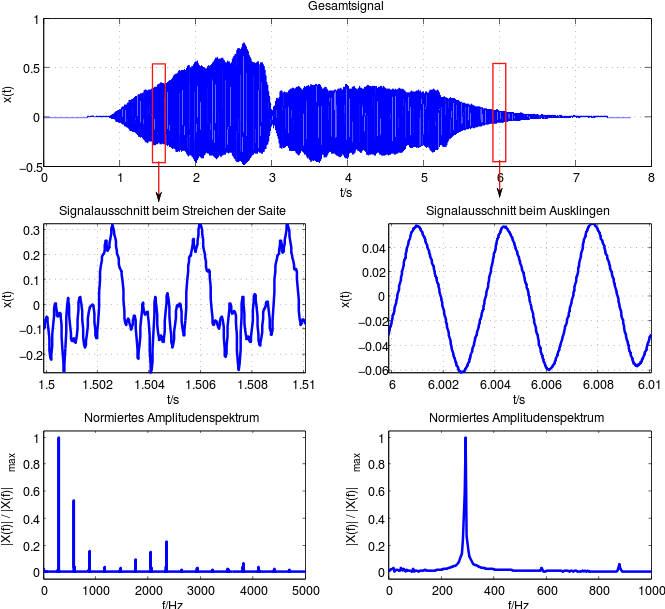
Als Beispiel soll das Amplitudenspektrum des folgenden Geigentons betrachtet werden
Das Spektrum des Geigentons ist abhängig von dem Zeitabschnitt, den man zur Analyse wählt. Betrachtet man einen Signalausschnitt, der während des Streichens der Saiten aufgenommen wurde, so erkennt man außer der Grundfrequenz von f0=294 Hz deutliche Frequenzanteile der ganzzahligen Vielfachen fn = n f0. Diese lassen sich dadurch erklären, dass die Saite nicht nur in ihrer Grundwelle schwingt, bei die Saite auf ihrer gesamten Länge eine Auslenkung erfährt, sondern sich ebenfalls Schwingungen mit Knotenpunkten bei 1/2, 1/3, 1/4, ... der Saitenlänge ausbilden. Die Schwingung bei einem Vielfachen des Grundtons heißt im musikalischen Sprachgebrauch Oberton. Die Ausprägung der einzelnen Obertone wird durch die Gesamtanordnung (Saite, Resonanzkörper, Anstreichen) der Saite bestimmt.
Im Gegensatz dazu zeigt der Signalausschnitt, der das Ausklingens des Tones berücksichtigt, keine markanten Obertonanteile auf.
Literatur
- DIN 13320, Spektren und Übertragungskurven, Begriffe, Darstellung
Siehe auch
Wikimedia Foundation.