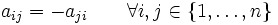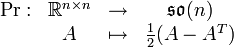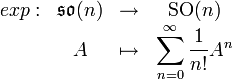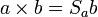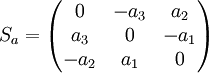- Schiefsymmetrisch
-
Eine schiefsymmetrische Matrix (bzw. antisymmetrische Matrix) ist eine Matrix, die gleich dem Negativen ihrer Transponierten ist.
Mathematisch:
- AT = − A
bzw. für die Einträge
Inhaltsverzeichnis
Eigenschaften
Körpercharakteristik ungleich 2
Eigenschaften für Körper
 der Charakteristik ungleich 2:
der Charakteristik ungleich 2:- Die Einträge auf der Hauptdiagonalen sind Null
- Die Determinante schiefsymmetrischer Matrizen mit ungerader Dimension ist wegen
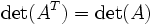 gleich Null.
gleich Null.
Vektorraum
Die schiefsymmetrischen Matrizen bilden einen Vektorraum der Dimension
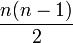 . Ist der Körper
. Ist der Körper 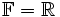 , so bezeichnet man diesen Vektorraum mit
, so bezeichnet man diesen Vektorraum mit 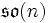 . Die Bezeichnung rührt daher, dass dieser Vektorraum die Lie-Algebra der Lie-Gruppe
. Die Bezeichnung rührt daher, dass dieser Vektorraum die Lie-Algebra der Lie-Gruppe 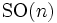 (Spezielle orthogonale Gruppe) ist.
(Spezielle orthogonale Gruppe) ist.Die orthogonale Projektion vom Raum der Matrizen in den Raum der schiefsymmetrischen Matrizen ist bzgl. des kanonischen Skalarprodukts gerade
Der orthogonale Rest ist die symmetrische Matrix
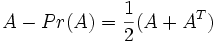 .
.
Exponentialabbildung
Die Abbildung
konvergiert, ist surjektiv und beschreibt gerade die Exponentialabbildung an der Einheitsmatrix In (siehe auch Spezielle orthogonale Gruppe).
Kreuzprodukt
Die schiefsymmetrische Matrix kann verwendet werden um das Kreuzprodukt als Matrixmultiplikation auszudrücken:
Dabei ist die schiefsymmetrische Matrix Sa definiert als:
Auf diese Weise kann eine Formel mit Kreuzprodukt differenziert werden, etwa zur Berechnung der Fehlerfortpflanzung.
Siehe auch
Wikimedia Foundation.