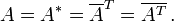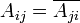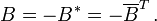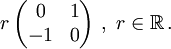Antihermitesche Matrix

Eine Matrix A heißt hermitesch (nach Charles Hermite) oder selbstadjungiert genau dann, wenn sie gleich ihrer (hermitesch) Adjungierten A ^* , also gleich der transponierten und komplex konjugierten Matrix ist. D. h.

$A = A^* = \overline A^T = \overline{A^T}\,.$

Beachte: Für die adjungierte Matrix finden sich auch die Bezeichnungen A^H und A^†, für die komplex konjugierte Matrix früher auch A^* (Vorsicht!).

Für die Elemente einer hermiteschen Matrix gilt also:

$A_{ij} = \overline{A_{ji}}$

Anders formuliert ist eine Matrix A genau dann hermitesch, wenn ihre Transponierte gleich ihrer komplex Konjugierten ist, d.h. $A^{\mathrm T} = \overline A\,$.

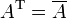Eigenschaften:

1. Die Matrix ist quadratisch.
2. Die Hauptdiagonalelemente sind reell.
3. Der Realteil ist symmetrisch, 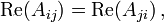$\mathrm{Re}(A_{ij}) = \mathrm{Re}(A_{ji}) \,,$ der Imaginärteil ist schiefsymmetrisch,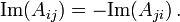 $\mathrm{Im}(A_{ij}) = - \mathrm{Im}(A_{ji})\,.$
4. Die Eigenwerte hermitescher Matrizen sind reell, die Eigenvektoren bilden ein Orthogonalsystem.
5. Hermitesche Matrizen lassen sich immer diagonalisieren.
6. Im Reellen fallen die Begriffe hermitesch und symmetrisch zusammen. Reelle symmetrische Matrizen lassen sich reell diagonalisieren.

Eine Matrix B heißt schiefhermitesch oder antihermitesch genau dann, wenn sie gleich ihrer negativen Adjungierten ist:

$B = -B^* = -\overline B^T\,.$

Eigenschaften:

1. Die Matrix ist quadratisch.
2. Die Hauptdiagonalelemente sind rein imaginär.
3. Der Realteil ist schiefsymmetrisch, der Imaginärteil ist symmetrisch.
4. Die Eigenwerte schiefhermitescher Matrizen sind rein imaginär, die Eigenvektoren bilden ein Orthonormalsystem.
5. Antihermitesche Matrizen lassen sich immer diagonalisieren.
6. Im Reellen fallen die Begriffe schiefhermitesch und schiefsymmetrisch zusammen. Reelle schiefsymmetrische Matrizen lassen sich durch reellen Basiswechsel in blockdiagonale Form bringen mit Blöcken

$r\,\begin{pmatrix}0&1\\-1&0\end{pmatrix}\ ,\ r\in\mathbb{R}\,.$

Siehe auch

• Glossar mathematischer Attribute#hermitesch