Sesquilinear — Als Sesquilinearform (lat. sesqui = anderthalb) bezeichnet man in der linearen Algebra eine Funktion, die zwei Vektoren einen Skalarwert zuordnet, und die linear in einem, semilinear im anderen ihrer beiden Argumente ist. Die beiden Argumente… … Deutsch Wikipedia
Antilinear — Als Semilinearform bezeichnet man in der linearen Algebra eine semilineare Abbildung aus einem Vektorraum in den diesem zugrundeliegenden Skalarkörper; relevant sind Semilinearformen lediglich über dem Körper C der komplexen Zahlen. Eine… … Deutsch Wikipedia
Konjugiert linear — Als Semilinearform bezeichnet man in der linearen Algebra eine semilineare Abbildung aus einem Vektorraum in den diesem zugrundeliegenden Skalarkörper; relevant sind Semilinearformen lediglich über dem Körper C der komplexen Zahlen. Eine… … Deutsch Wikipedia
Semilinearform — Als Semilinearform bezeichnet man in der linearen Algebra eine semilineare Abbildung aus einem Vektorraum in den diesem zugrundeliegenden Skalarkörper; relevant sind Semilinearformen lediglich über dem Körper C der komplexen Zahlen. Eine… … Deutsch Wikipedia
Banach-Algebra — berührt die Spezialgebiete Mathematik Topologie Abstrakte Algebra Lineare Algebra Funktionalanalysis ist Spezialfall von Abels … Deutsch Wikipedia
Banachalgebra — Banachalgebren (nach Stefan Banach) sind mathematische Objekte der Funktionalanalysis, die einige bekannte Funktionenräume und Operatorenalgebren anhand wesentlicher gemeinsamer Eigenschaften verallgemeinern, z. B. Räume stetiger oder… … Deutsch Wikipedia
Gelfand-Spektrum — Banach Algebra berührt die Spezialgebiete Mathematik Topologie Abstrakte Algebra Lineare Algebra Funktionalanalysis ist Spezialfall von Abels … Deutsch Wikipedia
Sesquilinearform — Als Sesquilinearform (lat. sesqui = anderthalb) bezeichnet man in der linearen Algebra eine Funktion, die zwei Vektoren einen Skalarwert zuordnet, und die linear in einem, semilinear im anderen ihrer beiden Argumente ist. Die beiden Argumente… … Deutsch Wikipedia
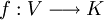genügt den beiden folgenden Bedingungen, die ganz allgemein eine semilineare Abbildung kennzeichnen: für alle x, y aus V und alle λ aus K gilt:
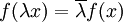, wobei 
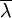das komplex Konjugierte von λ bezeichne.