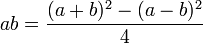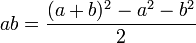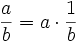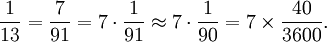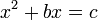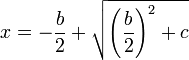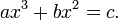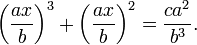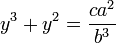Babylonische Zahlen

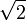Babylonische Keilschrifttafel YBC 7289 mit Anmerkungen. Die waagrechte Diagonale zeigt $\sqrt2$ mit vier Ziffern im Sexagesimalsystem, die etwa sechs Dezimalstellen entsprechen.
1 + 24/60 + 51/60² + 10/60³ = 1.41421296...
. Die Zahl darunter (42;25,35) ist die Diagonale eines Quadrates mit der Seitenlänge 30. (Bild von Bill Casselman)

Die Babylonische Mathematik wurde von den verschiedenen Bewohnern des Zweistromlandes (Mesopotamien, heute Irak) entwickelt. Ihr Beginn lag vermutlich in den Tagen der frühen Sumerer, und ihre Entwicklung setzte sich bis zur Eroberung von Babylon durch die Perser im Jahr 539 v. Chr. fort. Im Gegensatz zur Mathematik der Ägypter, von der wegen der empfindlichen Papyri nur wenige Quellen existieren, liegt von der babylonischen Mathematik ein Bestand von etwa 400 Tontafeln vor, der seit etwa 1850 ausgegraben wurde. Darauf beruht unser Wissen. Die Aufzeichnungen wurden mit Keilschrift in den noch weichen Ton geritzt und gebrannt oder in der Sonne getrocknet. Die Mehrzahl der gefundenen Tafeln stammen aus dem Zeitraum zwischen 1800 und 1600 v. Chr. und behandeln Themen wie Brüche, Algebra, quadratische und kubische Gleichungen und Pythagoreische Tripel (Plimpton 322). Auf der Tafel YBC 7289 findet sich eine Berechnung der 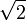$\sqrt2$ mit einer Genauigkeit von sechs Dezimalstellen.

Babylonisches Zahlensystem

Für die Darstellung von Zahlen wurde ein voll ausgebildetes Stellenwertsystem benutzt. Zahlen wurden im Sexagesimalsystem dargestellt, ein Stellenwertsystem zur Basis 60. Reste dieses Zahlensystems finden sich noch heute in unserer Darstellung von Winkeln (1° = 60’, 1' = 60’’) und Uhrzeiten. Da 60 = 4*3*5 als Teiler die Zahlen 1, 2, 3, 4, 5, 6, 10, 12, 15, 20 und 30 hat, können wesentlich mehr Zahlen als im Dezimalsystem in endlicher Darstellung geschrieben werden, was numerische Berechnungen sehr erleichtert hat. Zahlen wurden ziffernweise wie heute von links nach rechts geschrieben, wobei links die Ziffern mit größerem Stellenwert standen.

Ziffer von 1 bis 59:

Eine Ziffer für die Null kannten die Babylonier nicht. Sie wurde nicht als Zahl angesehen, sondern als nicht vorhanden sein einer Zahl und mit einem Leerzeichen dargestellt.

Es standen Formeln zur Flächen- und Volumenberechnung zur Verfügung. Für die Zahl π wurde 3 als Näherung benutzt. Auf einer neuerdings gefundenen Tafel ist ein besserer Näherungswert 3 1/8 angegeben.

Der Satz des Pythagoras war bekannt, aber nur hinsichtlich seiner Anwendung, nicht im Sinne eines mathematischen Beweises.

Auch die Messung des Erddurchmessers gelang schon babylonischen Astronomen. Man vermutet sogar, dass die heute Eratosthenes zugeschriebene Messung gar nicht von ihm ausgeführt wurde, sondern dass ihm eine ältere babylonische Messung bekannt war, die zwischen dem Berg Ararat und einer Hauptstadt im Zweistromland durchgeführt worden war, von Eratosthenes nach Ägypten übertragen wurde und als eigene Leistung beansprucht wurde.

Sumerische Mathematik (3000-2300 v. Chr.)

Die ältesten Zeugnisse schriftlich überlieferter Mathematik stammen von den Sumerern, die in Mesopotamien die früheste bekannte Kultur entwickelt haben. Aus dieser Zeit stammt ein leistungsfähiges Masssystem. Seit 2600 sind Multiplikationstabellen, geometrische und arithmetische Aufgaben nachgewiesen.

Ältere Babylonische Mathematik (2000–1600 v. Chr)

Aus dieser Epoche stammen die meisten der aufgefundenen Tontafeln zur Mathematik. Der Inhalt der Tafeln besteht aus Listen und Tabellen, in anderen Fällen behandeln sie Probleme und ausgearbeitete Lösungen.

Arithmetik

Zur Unterstützung der Arithmetik wurden vorgefertigte Tabellen benutzt. So finden sich auf zwei Tafeln, die in Senkerah am Euphrat im Jahr 1854 gefunden wurden und auf das Jahr 2000 v. Chr. datiert wurden, Listen mit allen Quadratzahlen bis 59 und Kuben bis 32. Die Quadratzahlen, speziell die Viertelquadrattabelle, ermöglichten das Berechnen von Produkten mit einer Addition und zwei Subtraktionen, sowie dem Aufsuchen zweier Quadrate in einer Quadratzahltabelle mit den Formeln

$ab = \frac{(a + b)^2 - (a - b)^2}{4}$

$ab = \frac{(a + b)^2 - a^2 - b^2}{2}$

(Viertelquadratmethode). Statt z. B. 3*6 direkt zu berechnen, berechnet man 3 + 6 = 9 und 6 - 3 = 3 (größere minus kleinere!) und schlägt die Viertelquadrate von 9 und 3 in der Tabelle (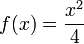$f (x) = \frac{x^2}{4}$) nach. Ergebnis: 20 und 2. Diese beiden Zahlen werden subtrahiert und ergeben das Produkt 20 - 2 = 18.

Die Division wurde nicht mit einem direkten Algorithmus durchgeführt, sondern mit der Formel

$\frac{a}{b} = a \cdot \frac{1}{b}$

auf die Multiplikation zurückgeführt. Dazu standen ausgedehnte Tabellen mit den Reziprokwerten zur Verfügung.

Die Reziprokwerte von 7, 11, 13 u. ä. haben im Sexagesimalsystem keine endliche Darstellung mehr. Deshalb wurden z. B. für 1/13 Approximationen benutzt:

$\frac{1}{13} = \frac{7}{91} = 7 \cdot \frac {1}{91} \approx 7 \cdot \frac{1}{90}=7 \times \frac{40}{3600}.$

Algebra

Quadratische Gleichungen wurden mit der auch heute noch von allen Schülern zu lernenden Formel gelöst. Da keine negativen Zahlen zur Verfügung standen, wurde etwa

$\ x^2 + bx = c$

mit nicht notwendig ganzzahligem, jedoch positivem b und c als

$x = - \frac{b}{2} + \sqrt{ \left ( \frac{b}{2} \right )^2 + c}$

angegeben. Die (eindeutig positive) Wurzel wurde der Quadrattabelle entnommen.

Auch die Lösung kubischer Gleichungen war bekannt. Dazu wurden n³+n² tabelliert. Zur Lösung von

$\ ax^3 + bx^2 = c.$

wurde die Gleichung mit a² multipliziert und durch b³ dividiert mit dem Ergebnis

$\left ( \frac{ax}{b} \right )^3 + \left ( \frac {ax}{b} \right )^2 = \frac {ca^2}{b^3}.$

Die Substitution y = ax/b ergibt

$y^3 + y^2 = \frac {ca^2}{b^3}$

Das kann nach y aufgelöst werden, wenn man n³+n² in der Tabelle nachschlägt, um den besten Wert für die rechte Seite aufzufinden. (Beispiel: 3*x^3 + 4*x^2 = 475; y^3+y^2 = 475*9/64 = 67; Die Tabelle liefert 3*x/4 = 3,7 und x = 5,0)

Die Rechnung wurde ohne algebraische Notation ausgeführt, was auf ein bemerkenswert tiefes Verständnis der zugrundeliegenden Mathematik hinweist. Für eine Kenntnis der allgemeinen kubischen Gleichung gibt es keine Hinweise.

Wie die relative bekannte Tontafel YBC 7289 (siehe [1] und [2]) beweist, konnten nach der Methode von Heron Quadratwurzeln mit hoher Genauigkeit berechnet werden.

Resumée: Es wurden komplexe Rechnung mit reellen Zahlen unter Verwendung von Tabellen durchgeführt. Zum Nachvollziehen sei ein kurzer Ausschnitt solcher Tabellen angegeben:

 n n^2 n^2/4   1/n   n^2+n^3  
 
 1   1   0 1,000000     2
 2   4   1 0,500000    12
 3   9   2 0,333333    36
 …
 3,75                  66,8
 …
 4  16   4 0,250000    80
 5  25   6 0,200000   150
 6  36   9 0,166667   252
 7  49  12 0,142857   392
 8  64  16 0,125000   576
 9  81  20 0,111111   810
10 100  25 0,100000  1100
 …

Geometrie

Die allgemeinen Regeln zur Flächen- und Volumenberechnung waren bekannt. Der Umfang U eines Kreises mit Durchmesser d wurde mit U = 3 * d und die Fläche A mit A = U * U / 12 angenommen. Beides geht mit der schlechten Näherung Pi = 3. Der Satz des Pythagoras wurde benutzt, aber nicht bewiesen; die Idee von Beweisen wurde erst von den Griechen entwickelt. Es existieren Tabellen mit den pythagoreischen Zahlentripeln wie 3, 4, 5.

Chaldäische Mathematik (626-539 v. Chr.)

Die chaldäische Periode ist diejenige des Neubabylonischen Reichs (626-539 v. Chr.). Dies war die zweite Blütezeit der Stadt Babylon. Die Stadt war Hauptstadt des Reichs und Zentrum der Wissenschaft. Die Quellenlage für diese Zeit ist jedoch ungünstiger.

Seit der Wiederentdeckung der babylonischen Kultur ist offensichtlich geworden, dass die griechischen Astronomen, besonders Hipparchos, über Informationen aus chaldäischen Quellen verfügten.

Franz Xaver Kugler wies in seinem Buch Die Babylonische Mondrechnung nach, dass Mondphasen schon in babylonischen Ephemeridentabellen auftauchen, die nach Ptolemäus (Almagest IV.2) von Hipparchos und ihm selbst unter Berücksichtigung älterer Beobachtungen der „Chaldäer“ verbessert wurden. Nach Kugler tauchen diese Werte in einer Tafelsammlung auf, die heute als „System B“ bekannt ist und die manchmal dem Astronomen Kiddinu zugeschrieben wird. Offensichtlich haben Ptolemäus und Hipparchos die älteren Werte lediglich durch aktuelle Beobachtungen überprüft.

Wir wissen, dass Hipparchos und später Ptolemäus über im Wesentlichen vollständige Listen von Finsternissen über mehrere Jahrhunderten verfügt haben. Diese Listen stammen wahrscheinlich von Tontafeln, die sämtliche relevanten Beobachtungen enthalten, die von den Chaldäern routinemäßig aufgezeichnet wurden. Erhaltene Tafeln sind zwischen 652 v. Chr. bis 130 n. Chr. datiert, aber die Aufzeichnungen gingen wahrscheinlich zurück bis in die Regierungszeit des Königs Nabonassar von Babylon. Bei Ptolemäus beginnt die Aufzeichnung am ersten Tag des ägyptischen Kalenders der ersten Regierungsjahren von Nabonassar, also am 26. Februar 747 v. Chr.

Die Rohdaten waren wahrscheinlich schwer benutzbar, sodass Exzerpte hergestellt wurden. So hat man z. B. Tafeln mit allen Finsternisereignissen aufgefunden. Konkret gibt es eine Tafel mit allen Finsternissen eines Saroszyklus. Damit konnten periodische Wiederholungen astronomischer Ereignisse identifiziert werden. Im System B wurde folgende Perioden gefunden (Almagest IV.2):

• 223 synodische Monate = 239 anomalistische Monate = 242 drakonische Monate. Diese Periode heißt heute der Saroszyklus und wird zur Vorhersage von Finsternissen benutzt.
• 251 synodische Monate = 269 anomalistische Monate
• 5458 synodische Monate = 5923 drakonische Monate
• 1 synodischer Monat = 29;31:50:08:20 Tage (sexagesimal; Dezimalwert: 29,53059413… Tage = 29 Tage 12 Stunden 44 min 3⅓ s)

Von den Babyloniern wurden alle Perioden in synodischen Monaten ausgedrückt, da wahrscheinlich ein lunisolarer Kalender verwendet wurde. Verschiedene Beziehungen von Phänomenen im Jahresverlauf führten zu mehreren Werten der Jahreslänge.

Auch für andere Planeten waren mehrere Messwerte für deren Umläufe um die Sonne bekannt. Die Werte, die Ptolemäus dem Astronomen Hipparchos im Almagest IX.3 zuschreibt, existierten schon auf älteren babylonischen Tafeln als Voraussagen.

Unklar ist, wann, inwieweit und auf welchen Wegen Teile dieses Wissens den Griechen zugänglich wurden. Dies war nur dadurch möglich, dass babylonische Gelehrte Werke in griechischer Sprache verfassten, denn die Griechen pflegten keine Fremdsprachen zu lernen und konnten keine Keilschrifttexte lesen.

Weblinks

• Elemente vorantiker Mathematik Vergleich zwischen babylonischen und ägyptischen Rechentechniken
• Babylonische Zahlen Private Seite von Wolfgang Appell, Lehrer für Mathematik an der Staatlichen Realschule Ebermannstadt