Sierpinski-Problem

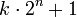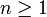Eine Sierpinski-Zahl (benannt nach dem polnischen Mathematiker Wacław Sierpiński) ist eine natürliche, ungerade Zahl k, deren Folge aus Zahlen der Form $k\cdot 2^n+1$ mit $n \ge 1$ keine Primzahlen enthält.

Gegenbeispiel

Die Zahl k = 19 ist keine Sierpinski-Zahl, da in der Folge 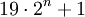$19\cdot 2^n+1$ wenigstens eine Primzahl auftritt: 39, 77, 153, 305, 609, 1.217,...

Eine solche auftauchende Primzahl nennt man Prothsche Primzahl.

Sierpinski-Problem

Das Sierpinski-Problem lautet: Welche ist die kleinste Sierpinski-Zahl?. 1967 hat John Selfridge gezeigt, dass 78.557 eine Sierpinski-Zahl ist. Es ist jedoch noch nicht bekannt, ob 78.557 die kleinste Sierpinski-Zahl ist. Es wird aber vermutet, dass es sich um die kleinste Sierpinski-Zahl handelt.

Um den Beweis durchzuführen, muss für jedes k kleiner als 78.557 eine Zahl n gefunden werden, so dass die resultierende Proth-Zahl N = k2ⁿ + 1 eine Primzahl ist. Dieser Beweis ist (Stand 11/2007) bereits für alle k bis auf 6 Zahlen erfolgt: 10.223, 21.181, 22.699, 24.737, 55.459 und 67.607.

Riesel-Zahl

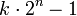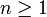Eine Riesel-Zahl (benannt nach dem schwedischen Mathematiker Hans Riesel) ist eine natürliche, ungerade Zahl k, deren Folge aus Zahlen der Form $k\cdot 2^n-1$ mit $n \ge 1$ keine Primzahlen enthält.

Gegenbeispiel

Die Zahl k = 23 ist keine Riesel-Zahl, da in der Folge 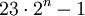$23\cdot 2^n-1$ wenigstens eine Primzahl auftritt: 45, 91, 183, 367

Die kleinste Riesel-Zahl

Riesel selbst fand 1956 mit 509.203 eine Riesel-Zahl. Es ist jedoch noch nicht bekannt, ob 509.203 die kleinste Riesel-Zahl ist.

Weblinks

• ein distributed-computing Projekt das sich mit dem Sierpinski-Problem beschäftigt (englisch)
• ein weiteres distributed-computing Projekt das sich mit dem Sierpinski-Problem beschäftigt (englisch)
• distributed-computing Projekt für das Riesel-Problem
• The Prime Glossary
• Status des Sierpinski-Problems
• Status des Riesel-Problems