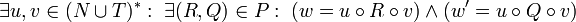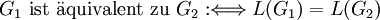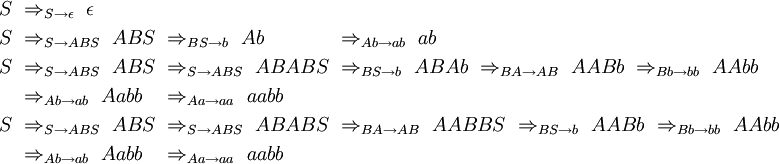Startvariable

Formale Grammatiken sind mathematische Modelle von Grammatiken, die mit Hilfe des Semi-Thue-Systems angegeben werden und durch die formale Sprachen beschrieben und erzeugt werden können. Sie werden in der theoretischen Informatik, insbesondere in der Berechenbarkeitstheorie, und im Compilerbau angewandt, um zum einen eine formale Sprache eindeutig zu beschreiben (d. h. um eindeutig festzulegen, ob ein Wort Element einer Sprache ist, oder nicht) und um zum anderen Eigenschaften dieser formalen Sprachen zu untersuchen bzw. zu beweisen. Formale Grammatiken werden mit Hilfe der Chomsky-Hierarchie klassifiziert.

Definition

Eine formale Grammatik ist ein 4-Tupel G = (N,T,P,S) bestehend aus:

• N eine nichtleere, endliche Menge (ein Alphabet) von Nichtterminalsymbolen
• T eine nichtleere, endliche Menge (ein Alphabet) von Terminalsymbolen, wobei 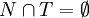$N \cap T = \emptyset$ ist, also die Mengen N und T disjunkt sind. Es gibt somit kein Symbol, das sowohl Nichtterminal- als auch Terminalsymbol ist.
• P eine nichtleere, endliche Menge von Produktionsregeln, welche eine Teilmenge der Menge 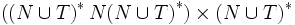$\left( \left( N \cup T \right)^* N ( N \cup T \right)^*) \times \left( N \cup T \right)^*$ ist.
• S dem Startsymbol, das zur Menge der Nichtterminalen gehört ($S \in N$)

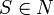Die Menge aller terminaler und aller nichtterminaler Symbole 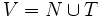$V = N \cup T$ einer Grammatik G wird Vokabular dieser Grammatik genannt.

Elemente einer formalen Grammatik

Nichtterminalsymbole

Ein Nichtterminalsymbol (auch Nichtterminal oder Variable genannt) ist ein Symbol, welches zur Erzeugung der formalen Sprache, die durch die Grammatik beschrieben werden soll, verwendet wird, aber im Gegensatz zu Terminalsymbolen kein Symbol ist, welches in den Wörtern der erzeugten Sprache vorkommt. Nichtterminale werden gewöhnlich durch Großbuchstaben repräsentiert oder durch spitze Klammern gekennzeichnet (<Nichtterminal>).

Terminalsymbole

Terminalsymbole (auch Terminalzeichen oder kurz Terminale genannt) sind diejenigen Symbole, aus denen sich die Worte der zu erzeugenden formalen Sprache zusammensetzen. Sie werden in der Regel durch Kleinbuchstaben repräsentiert. Ein einzelnes Terminalsymbol kann bei der Erzeugung der durch die Grammatik beschriebenen Sprache nicht durch eine Produktionsregel ersetzt werden.

Produktionsregeln

Eine Produktionsregel (auch Regel oder Produktion genannt) ist ein geordnetes Paar (R,Q), wobei R ein aus Terminale und Nichtterminale bestehendes Wort ist, welches mindestens ein Nichtterminalsymbol enthält (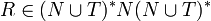$R \in (N \cup T)^\ast N (N \cup T)^\ast$), und Q ein beliebiges, aus terminalen und nichtterminalen Symbolen bestehendes Wort ist (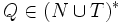$Q \in (N \cup T)^\ast$). R wird auch Prämisse und Q Konklusion der Produktionsregel (R,Q) genannt. Eine Produktionsregel (R,Q) wird oftmals mit Hilfe der Schreibweise 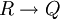$R \rightarrow Q$ notiert und eine Menge von Regeln 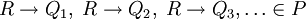$R \rightarrow Q_1,\; R \rightarrow Q_2,\; R \rightarrow Q_3, \ldots \in P$ wird oft durch die Schreibweise 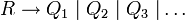$R \rightarrow Q_1 \;|\; Q_2 \;|\; Q_3 \;| \ldots$ abgekürzt.

Startsymbol

Das Startsymbol (auch Startvariable genannt) ist ein Nichtterminalsymbol, von welchem aus die Wörter der durch die Grammatik beschriebenen Sprache erzeugt werden. Zur Darstellung des Startsymbols wird meist das Zeichen S verwendet.

Die Erzeugung der von einer Grammatik beschriebenen Sprache

Eine Regel 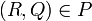$(R,Q) \in P$ einer gegebenen Grammatik G besagt, dass in einem Wort 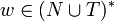$w \in (N \cup T)^\ast$ mit R als Infix, dieses durch das Wort Q ersetzt werden kann, so dass ein neues Wort 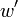$w^\prime$ mit Q als Infix entsteht. Man spricht hierbei auch davon, dass w in 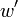$w^\prime$ mit der Grammatik G bzw. durch die Regel 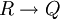$R \rightarrow Q$ übergeht, welches über die Schreibweisen 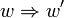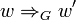$w \Rightarrow w^\prime$, $w \Rightarrow_G w^\prime$ bzw. 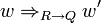$w \Rightarrow_{R \rightarrow Q} w^\prime$ notiert wird. Demnach ist ein solcher Übergang von w in 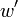$w^\prime$ eine Transitionsrelation, die für gegebene w und 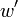$w^\prime$ genau dann definiert ist, wenn:

$\exists u,v \in (N \cup T)^\ast:\; \exists (R,Q) \in P:\; (w = u \circ R \circ v) \and (w^\prime = u \circ Q \circ v)$

Gibt es nun eine Folge von Wörtern 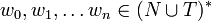$w_0, w_1, \ldots w_n \in (N \cup T)^\ast$, bei der gilt, dass für jede natürliche Zahl i mit 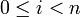$0 \le i &amp;lt; n$ das Wort w_i in w_{i + 1} übergeht (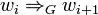$w_i \Rightarrow_G w_{i+1}$), so ist w_n in n Schritten aus w₀ ableitbar, was durch 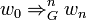$w_0 \Rightarrow_G^n w_n$ dargestellt wird. Eine solche Wortfolge 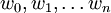$w_0, w_1, \ldots w_n$ wird Ableitung oder Rechnung von w₀ in w_n der Länge n genannt. Weiterhin heißt w in 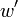$w^\prime$ ableitbar, wenn es mindestens ein 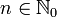$n \in \mathbb{N}_0$ gibt, so dass 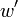$w^\prime$ in n Schritten aus w ableitbar ist. Wenn w in 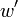$w^\prime$ ableitbar ist, so wird dies durch die Schreibweise 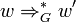$w \Rightarrow_G^\ast w^\prime$ dargestellt. Dabei wird zusätzlich definiert, dass für jedes Wort 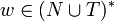$w \in (N \cup T)^\ast$ gilt, dass 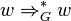$w \Rightarrow_G^\ast w$ ist, so dass die Relation 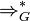$\Rightarrow_G^\ast$ die reflexiv-transitive Hülle der Relation 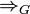$\Rightarrow_G$ ist.

Nun ist die von der Grammatik G erzeugte, formale Sprache L(G) diejenige Sprache, die aus allen Wörtern besteht, die zum einen nur aus Terminalsymbole bestehen und die zum anderen vom Startsymbol mit einer endlichen Anzahl von Schritten abgeleitet werden können:

$L \left( G \right) := \left\{ w \in T^* | S \Rightarrow_G^* w \right\}$

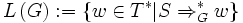
Dabei ist es egal, in welcher Reihenfolge die Produktionsregeln auf die abgeleiteten Wörter angewandt werden, oder ob es mehrere Möglichkeiten gibt, um ein Wort w aus S abzuleiten. Zwei Grammatiken G₁ und G₂ sind genau dann äquivalent, wenn die durch G₁ und G₂ erzeugten Sprachen gleich sind:

$G_1 \mathrm{\ ist\ \ddot{a}quivalent\ zu\ } G_2: \Longleftrightarrow L(G_1) = L(G_2)$

Beispiele

Wir betrachten die kontextsensitive Grammatik G mit den Terminalen {a,b}, den Nichtterminalen {S,A,B} mit dem Startsymbol S und den Regeln

$\begin{matrix}S&amp;amp;\to&amp;amp;ABS\\ S&amp;amp;\to&amp;amp;\varepsilon\\ BA&amp;amp;\to&amp;amp;AB\\ BS&amp;amp;\to&amp;amp;b\\ Bb&amp;amp;\to&amp;amp;bb\\ Ab&amp;amp;\to&amp;amp;ab\\ Aa&amp;amp;\to&amp;amp;aa\end{matrix}$

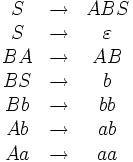
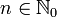Dabei ist $\varepsilon$ das leere Wort, welches ein Wort der Länge 0 ist. Diese Grammatik G definiert die Sprache aller Wörter der Form aⁿbⁿ mit $n \in \mathbb N_0$. So sind auf Grund der folgenden Ableitungen die Wörter ε, ab und aabb Elemente der durch G erzeugten Sprache:

$\begin{alignat}{3} S &amp;amp;\ \Rightarrow_{S \rightarrow \epsilon} \ \epsilon\\ S &amp;amp;\ \Rightarrow_{S \rightarrow ABS}\ ABS&amp;amp;&amp;amp;\ \Rightarrow_{BS \rightarrow b}\ Ab\qquad \quad\ \ \Rightarrow_{Ab \rightarrow ab}\ ab\\ S &amp;amp;\ \Rightarrow_{S \rightarrow ABS}\ ABS&amp;amp;&amp;amp;\ \Rightarrow_{S \rightarrow ABS}\ ABABS\ \Rightarrow_{BS \rightarrow b}\ ABAb\ \Rightarrow_{BA \rightarrow AB}\ AABb\ \Rightarrow_{Bb \rightarrow bb}\ AAbb\\ &amp;amp;\ \Rightarrow_{Ab \rightarrow ab}\ Aabb&amp;amp;&amp;amp;\ \Rightarrow_{Aa \rightarrow aa}\ aabb\\ S &amp;amp;\ \Rightarrow_{S \rightarrow ABS}\ ABS&amp;amp;&amp;amp;\ \Rightarrow_{S \rightarrow ABS}\ ABABS\ \Rightarrow_{BA \rightarrow AB}\ AABBS\ \Rightarrow_{BS \rightarrow b}\ AABb\ \Rightarrow_{Bb \rightarrow bb}\ AAbb\\ &amp;amp;\ \Rightarrow_{Ab \rightarrow ab}\ Aabb&amp;amp;&amp;amp;\ \Rightarrow_{Aa \rightarrow aa}\ aabb \end{alignat}$

Man beachte, dass es mehrere Ableitungen gibt, um das Wort aabb aus S abzuleiten. Eine weitere Grammatik zur Erzeugung der betrachteten Sprache 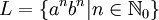$L = \{a^n b^n | n \in \mathbb{N}_0\}$, die kontextfrei ist, ist die Grammatik mit den Regeln: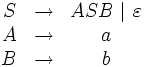

$\begin{matrix}S&amp;amp;\to&amp;amp; ASB\ |\ \varepsilon\\ A&amp;amp;\to&amp;amp;a\\ B&amp;amp;\to&amp;amp;b\end{matrix}$

oder kurz:

$\begin{matrix}S&amp;amp;\to&amp;amp;aSb\ |\ \varepsilon\end{matrix}$

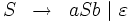
Man sieht, dass es zur Erzeugung einer Sprache mehrere (genaugenommen: abzählbar unendlich viele) Grammatiken gibt.

Siehe auch

• Graphgrammatik
• Backus-Naur-Form und Erweiterte Backus-Naur-Form
• Syntaxtheorie zu (formalen) Grammatiken in der Linguistik

Literatur

• Katrin Erk, Lutz Priese: Theoretische Informatik: eine umfassende Einführung. 2., erw. Auflage. Springer-Verlag, 2002, ISBN 3-540-42624-8, S. 53-61. 

Weblinks

• Website zum Thema Grammatik
• Vorlesungsskript zu formalen Grammatiken
• weiterer Vorlesungsskript