Summenhäufigkeitsfunktion

Eine Empirische Verteilungsfunktion F(t) - auch Summenhäufigkeitsfunktion oder Verteilungsfunktion der Stichprobe genannt - ist definiert als die Summe der relativen Häufigkeiten derjenigen Stichprobenwerte/Merkmalsausprägungen, die kleiner oder gleich t sind.

Die Definition der Empirischen Verteilungsfunktion kann in verschiedenen Schreibweisen erfolgen. Dabei ist die eine Variante mehr an die Bedürfnisse der deskriptiven Statistik und die andere mehr an die der Wahrscheinlichkeitstheorie angepasst. Die Definition in der deskriptiven Variante stellt quasi eine praxistaugliche Version dar, während die wahrscheinlichkeitstheoretische Variante zusammen mit einem Satz von Glivenko-Cantelli eine mathematische Begründung dafür liefert, warum es überhaupt Sinn hat mit einer Empirischen Verteilungsfunktion zu arbeiten.

Definition (deskriptive Variante)

Seien 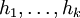$h_1, \ldots, h_k$ die relativen Häufigkeiten der reellen Merkmalsausprägungen 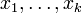$x_1, \ldots , x_k$ einer Stichprobe 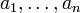$a_1, \ldots , a_n$ vom Umfang $n \in \mathbb{N}$. Dann heißt die durch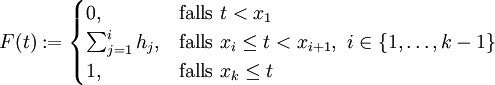

$F(t) := \begin{cases} 0, & \text{falls } t < x_1 \\ \sum_{j=1}^i h_j, & \text{falls } x_i \leq t < x_{i+1}, ~ i \in \{ 1, \ldots , k-1\} \\ 1, & \text{falls } x_k \leq t \end{cases}$

für alle 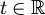$t \in \mathbb{R}$ definierte Funktion $F : \mathbb{R} \rightarrow [0,1]$ die Empirische Verteilungsfunktion (zur Stichprobe $a_1, \ldots , a_n$).

---

Die Empirische Verteilungsfunktion

$F_x : \mathbb{R} \rightarrow [0,1],\quad t \rightarrow F_x(t) = \sum_{j:a_j \leq t} {h_x(a_j)}$ ^[1]

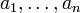ist eine Funktion aus der Deskriptiven Statistik. Sie dient der Visualisierung einer Stichprobe x. Die Funktion ordnet jeder Reellen Zahl t die Summe der Relativen Häufigkeiten h_x(a_j) derjenigen Zahlen aus der Stichprobe zu, die kleiner oder gleich groß wie t sind.

Definition (wahrscheinlichkeitstheoretische Variante)

Seien 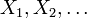$X_1, X_2, \dots$ reelle Zufallsvariablen, also messbare Abbildung von einem Wahrscheinlichkeitsraum (Ω,Σ,P) in den Maßraum 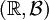$(\mathbb{R},\mathcal{B})$. Dann heißt die Abbildung

$F_n(t,\omega) := \frac{1}{n} \sum_{j=1}^n 1_{(-\infty, t ]} \left( X_j(\omega) \right), \qquad t \in \mathbb{R}, ~ \omega \in \Omega,$

die Empirische Verteilungsfunktion von X₁,...,X_n.

Quellen

1. ↑ Prof. Dr. N. Henze, Priv.-Doz. Dr. D. Kadelka. Skript zur Vorlesung Wahrscheinlichkeitstheorie und Statistik für Studierende der Informatik. Universität Karlsruhe, S. 11

• Bauer, Heinz: Wahrscheinlichkeitstheorie. Berlin - New York 2002
• Mayer, Horst: Beschreibende Statistik. München - Wien 1995

Siehe auch

• Histogramm
• deskriptive Statistik
• Gliwenko-Cantelli-Satz