- Ecke
-
Die Ecke, auch der Eckpunkt, ist in der Geometrie ein besonders ausgezeichneter Punkt der Grenzlinie oder -fläche eines Gebietes.
Die Ecken von zweidimensionalen Polygonen (Vielecken) sind die Punkte, an denen die begrenzenden Linien, die Seiten, aufeinandertreffen. Im Falle der dreidimensionalen Polyeder (Vielflächner) bezeichnet man die Punkte, an denen (mindestens) drei der begrenzenden Flächen aufeinandertreffen, als Ecken. Die Ecken von Polyedern sind Endpunkte der Kanten.
Im Falle eines konvexen n-dimensionalen Polytopes ist eine Ecke dadurch charakterisiert, dass sie nicht als echte Konvexkombination zweier verschiedener Punkte des Polytopes dargestellt werden kann (Extremalpunkt).
Für dreidimensionale Polyeder gibt es eine Gleichung, die einen Zusammenhang zwischen den Ecken, Kanten und Flächen eines beliebigen konvexen Polyeders beschreibt, den eulerschen Polyedersatz.
-
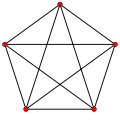
Ein regelmäßiges Fünfeck hat 5 Ecken und 5 Seiten.
-
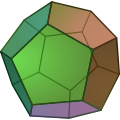
Ein regelmäßiges Dodekaeder hat 12 Flächen (daher sein Name), 20 Ecken und 30 Kanten.
Siehe auch
- In der Graphentheorie gibt es das verwandte Konzept der „Knoten“,
- in der projektiven Geometrie werden Punkte in allgemeiner Lage als Ecken bezeichnet. Sie bestimmen dort wichtige Figuren wie zum Beispiel das vollständige Viereck.
Literatur
- Johannes Böhm, Erhard Quaisser: Schönheit und Harmonie geometrischer Formen. Sphäroformen und symmetrische Körper. Akademischer Verlag, Berlin 1991, ISBN 3-05-500704-2.
- Dieter Grillmayer: Im Reich der Geometrie. Teil I: Ebene Geometrie. Books on Demand, Norderstedt 2009, ISBN 978-3-8370-2335-0.
- Erwin Gureczny: Polyeder. Bemerkungen über verschiedene Zugänge zu allgemeinen, regulären und halbregulären Polyedern, deren Existenz und Möglichkeiten der Konstruktion. Technische Universität Wien, Wien 1993.
- Mario Holzbauer: Vierdimensionale Polytope. Diplomarbeit. Technische Universität Wien, Wien 2007 (Mit umfangreichem Literaturverzeichnis).
-
Wikimedia Foundation.