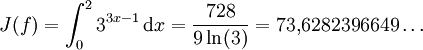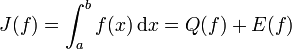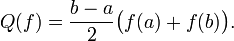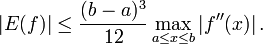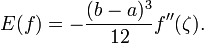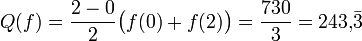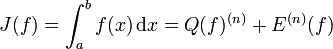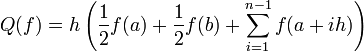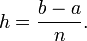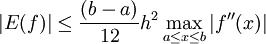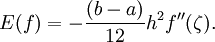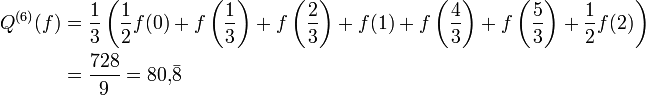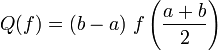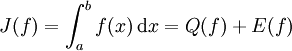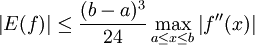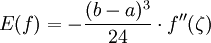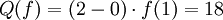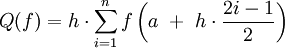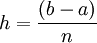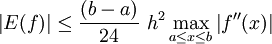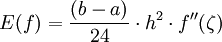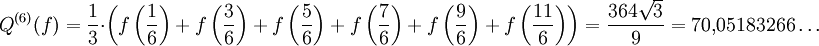Trapezformel

Die Trapezregel beschreibt ein mathematisches Verfahren, wie man das Integral einer Funktion im Intervall [a,b] numerisch annähert. Das entspricht der Fläche unter der Kurve f(x) bei kartesischer Darstellung.

Dazu ersetzt man die Fläche unter der Kurve durch ein Trapez, oder bei Stückelung des Intervalls durch mehrere Trapeze.

Man kann die Kurve f(x) näherungsweise durch eine Sehne zwischen den Funktionswerten an den Stellen a und b ersetzen. Dies führt zur Sehnentrapezformel. Man kann aber auch in der Mitte von [a,b] die Tangente an f(x) legen und erhält dann die Tangententrapezformel.

Beispiel

$J(f) = \int_{0}^{2}3^{3x-1} \, \mathrm{d}x = \frac{728}{9 \ln(3)} = 73{,}6282396649\dots$

Nun gilt es mit Hilfe der Trapezformel als Näherungsverfahren dieses Integral zu bestimmen.

Sehnentrapezformel

Sehnentrapez

$J(f) = \int_a^b f(x)\, \mathrm dx = Q(f) + E(f)$

Das Trapez wird gebildet aus der Grundlinie [a,b] (dem Intervall auf der x-Achse), den senkrechten Geraden [a,f(a)] und [b,f(b)] sowie der Sehne als Verbindungsgerade zwischen f(a) und f(b). Diese Sehne ersetzt die Kurve $f(x), x\in[a,b]$.

Die Sehnentrapezformel ergibt sich aus dem Flächeninhalt des beschriebenen Trapezes:

$Q(f) = \frac{b-a}2\bigl(f(a)+f(b)\bigr).$

Diese Formel sowie die folgenden können aus der „allgemeinen Quadraturformel für eine Teilfläche“ hergeleitet werden (siehe Numerische Quadratur).

Ist f zweimal stetig differenzierbar in [a,b], dann gilt für das Restglied E(f) die Abschätzung (siehe Numerische Quadratur)

$\left|E(f)\right| \le\frac{(b-a)^3}{12} \max_{a\le x\le b} \left|f''(x)\right|.$

Ist f zusätzlich noch reellwertig, dann gilt mit einer Zwischenstelle ζ aus [a,b]

$E(f) = -\frac{(b-a)^3}{12} f''(\zeta).$

Anschließend an das obige Beispiel:

$Q(f) = \frac{2-0}2 \bigl(f(0) + f(2)\bigr) = \frac{730}3 = 243{,}\bar{3}$

Zusammengesetzte Sehnentrapezformel

$J(f) = \int_a^b f(x)\,\mathrm dx = Q(f)^{(n)} + E^{(n)}(f)$

Um das Integral noch besser annähern zu können unterteilt man das Intervall [a,b] in n nebeneinanderliegende gleich große Teilintervalle der Länge 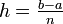$h=\tfrac{b-a}n$. In jedem Teilintervall wendet man die Sehnentrapezformel für die einzelnen Teilflächen an und addiert danach die entstandenen Näherungen. Damit erhält man die summierte (bzw. zusammengesetzte) Sehnentrapezformel:

$Q(f)=h\left(\frac 12 f(a) + \frac 12 f(b) + \sum_{i=1}^{n-1} f(a+ih)\right)$

mit

$h = \frac{b-a}n.$

Die Fehlerabschätzung für das Restglied lautet

$\left|E(f)\right|\le\frac{(b-a)}{12} h^2 \max_{a\le x\le b} \left|f''(x)\right|$

bzw. für reellwertige Funktionen mit einer Zwischenstelle ζ aus dem Intervall [a,b]

$E(f)= -\frac{(b-a)}{12} h^2 f''(\zeta).$

Anschließend an das obige Beispiel: Sei die Schrittweite 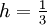$h = \tfrac 13$ und damit n = 6. Dann ist

$\begin{align} Q^{(6)}(f) &= \frac 13\left(\frac 12f(0) + f\left(\frac 13\right) + f\left(\frac 23\right) + f(1) + f\left(\frac 43\right) + f\left(\frac 53\right) + \frac 12 f(2) \right)\\ &= \frac{728}9 = 80{,}\bar{8} \end{align}$

Tangententrapezformel

Tangententrapez

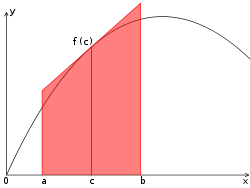
Die obere Seite des Trapezes wird hier gebildet, indem man in der Mitte des Intervalls [a,b] eine Tangente an f(x) legt. Die restliche Seiten sind die Grundlinie [a,b] (das Intervall auf der x-Achse) und die senkrechten Geraden an den Stellen a und b bis zur Tangente.

Die Tangententrapezformel ergibt sich aus dem Flächeninhalt des beschriebenen Trapezes:

$Q(f) = (b - a) \ f\left(\frac{a + b}{2} \right)$

Diese Formel - und auch die folgenden - kann man herleiten aus der „Allgemeinen Quadraturformel für eine Teilfläche“ (siehe Numerische Quadratur).

Damit lässt sich das Integral darstellen als

$J(f) = \int_{a}^{b}f(x)\, \mathrm{d}x = Q(f) + E(f)$

Ist f(x) zweimal stetig differenzierbar in [a,b], dann gilt für das Restglied E(f) folgende Abschätzung (siehe Numerische Quadratur):

$\left| E(f) \right| \le \frac{(b-a)^3}{24} \max_{a\le x \le b} {\left| f''(x) \right|}$

Ist f(x) zusätzlich noch reellwertig, dann gilt mit einer Zwischenstelle ζ aus [a,b]:

$E(f) = - \frac{(b-a)^3}{24} \cdot f''(\zeta)$

Anschließend an das obige Beispiel:

$Q(f) = (2-0) \cdot f(1) = 18$

Zusammengesetzte Tangententrapezformel

Um das Integral noch besser annähern zu können, unterteilt man das Intervall [a,b] in n nebeneinanderliegende gleich große Teilintervalle der Länge h. In jedem Teilintervall wendet man die Tangententrapezformel für die einzelnen Teilflächen an und addiert danach die entstandenen Näherungen. Damit erhält man die summierte Tangententrapezformel:

$Q(f)=h \cdot \sum_{i=1}^n f\left(a \ + \ h \cdot \frac{2i - 1}{2}\right)$

mit

$h = \frac{(b - a)}{n}$

Die Fehlerabschätzung für das Restglied lautet:

$\left| E(f) \right| \le {(b - a) \over 24} \ h^2 \max_{a\le x \le b} {\left| f''(x) \right|}$

bzw. für reellwertige Funktionen mit einer Zwischenstelle ζ aus dem Intervall [a,b]:

$E(f)={(b - a) \over 24} \cdot h^2 \cdot f''(\zeta)$

Anschließend an das obige Beispiel: Sei die Schrittweite 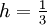  $h = \tfrac 13$ und damit n = 6

$Q^{(6)}(f) = \frac{1}{3} \cdot \left(f\left(\frac{1}{6}\right) + f\left(\frac{3}{6}\right) + f\left(\frac{5}{6}\right) + f\left(\frac{7}{6}\right) + f\left(\frac{9}{6}\right) + f\left(\frac{11}{6}\right) \right) = \frac{364 \sqrt 3}{9} = 70{,}05183266\dots$

Siehe auch

• Simpsonsche Formel (Kepler-Simpson-Regel)
• Romberg-Integration
• Keplersche Fassregel

Literatur

• Stoer: Numerische Mathematik, Springer-Verlag, Berlin, 2005, ISBN 3-540-21395-3