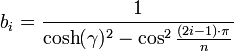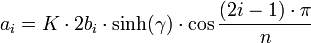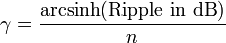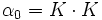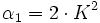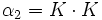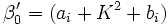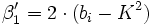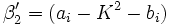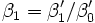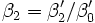- Tschebyschow-Filter
-
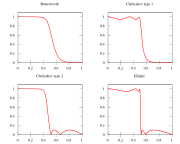
Tschebyscheff-Filter sind kontinuierliche Frequenzfilter, die auf ein möglichst scharfes Abknicken des Frequenzganges bei der Grenzfrequenz ausgelegt sind. Dafür verläuft die Verstärkung im Durchlassbereich oder im Sperrbereich nicht monoton, sondern besitzt eine festzulegende Welligkeit. Innerhalb einer Ordnung ist der Abfall umso steiler, je größer die zugelassene Welligkeit ist. Sie sind benannt nach Pafnuti Lwowitsch Tschebyschow (früher transkribiert als Tschebyscheff).
Es wird zwischen Tschebyscheff-Filtern vom Typ I und vom Typ II unterschieden. Tschebyscheff-Filter vom Typ I besitzen im Durchlassbereich einen oszillierenden Verlauf der Übertragungsfunktion. Tschebyscheff-Filter vom Typ II besitzen die Welligkeit der Übertragungsfunktion im Sperrbereich.
Inhaltsverzeichnis
Übertragungsfunktion
Für den Bereich
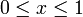 besitzen die Tschebyscheff-Polynome Tn die gewünschten Eigenschaften. Für
besitzen die Tschebyscheff-Polynome Tn die gewünschten Eigenschaften. Für 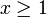 wachsen die Tschebyscheff-Polynome monoton.
wachsen die Tschebyscheff-Polynome monoton.Um mit Hilfe der Tschebyscheff-Polynome einen Tiefpass herzustellen, setzt man
mit k so gewählt, dass für x=0
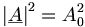 wird ε Maß der Welligkeit.
wird ε Maß der Welligkeit.Koeffizienten
Bringt man die Übertragungsfunktion in die Form
ergeben sich für die Koeffizienten ai und bi folgende Beziehungen:
Ordnung n des Filters gerade:
Ordnung n des Filters ungerade:
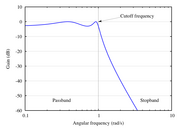
Diese Koeffizienten sind so gewählt, dass die Grenzfrequenz ωg auf die letzte Frequenz normiert ist, an der die gewählte Verstärkung das letzte Mal angenommen wird.
Eigenschaften
Das Tschebyscheff-Filter besitzt folgende Eigenschaften:
- welliger Frequenzverlauf je nach Typus im Durchlassbereich oder im Sperrbereich.
- sehr steiles Abknicken bei der Grenzfrequenz, verbessert sich mit der Ordnung und der Welligkeit.
- beträchtliches Überschwingen bei der Sprungantwort, verschlechtert sich mit der Ordnung und Welligkeit.
- lässt man die Welligkeit gegen 0 gehen, geht das Tschebyscheff-Filter in ein Butterworth-Filter über.
- keine konstante Gruppenlaufzeit im Durchlassbereich.
Digitale Realisierung
Für eine digitale Realisierung des Tschebyscheff-Filters transformiert man zunächst die einzelnen Biquads mittels bilinearer Transformation und kaskadiert diese mit den entsprechenden Koeffizienten ai und bi. Im folgenden ist dies für ein Tiefpassfilter mit gerader Ordnung n durchgeführt worden.
Die Z-Transformierte eines Biquads sieht generell wie folgt aus:
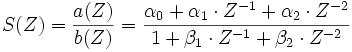 .
.
Diese Gleichung transformiert sich in den Zeitbereich wie folgt:
Die Koeffizienten αi und βi berechnen sich aus den Koeffizienten ai und bi folgendermaßen:
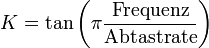 (Prewarp der Frequenz)
(Prewarp der Frequenz)
γ ist dabei ein Maß für das Überschwingen:
Die Koeffizienten berechnen sich dann zu:
Um Filter höherer Ordnung zu realisieren, braucht man nur mehrere Biquad-Sektionen zu kaskadieren. Die Umsetzung digitaler Tschebyscheffilter erfolgt in IIR-Filterstrukturen (rekursive Filterstruktur).
Siehe auch
Wikimedia Foundation.

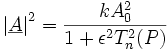
![A[P] = \frac{A_0}{\prod_i (1 + a_i P + b_i P^2)}](/pictures/dewiki/101/eb4fecf99f43a477313ce2352425f9a7.png)
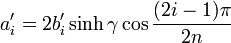
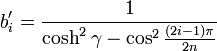
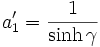
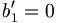
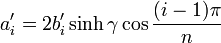
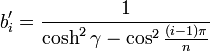
![y[n]=\alpha_0 \cdot x[n] + \alpha_1 \cdot x[n-1] + \alpha_2 \cdot x[n-2] - \beta_1 \cdot y[n-1] - \beta_2 \cdot y[n-2]](/pictures/dewiki/56/8d58a01b531f52c7afea043d69c50888.png)