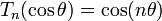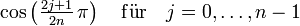- Tschebyscheff-Polynom
-
Tschebyschow-Polynome (nach Pafnuti Lwowitsch Tschebyschow, oft auch als Tschebyscheff, Tschebycheff, Tschebyschew, Tschebyschev oder Chebychev in der Literatur zu finden) sind Polynome Tn(x), die sich als Lösung der Tschebyschow-Differentialgleichung
ergeben. Die Funktionen
und
bilden ein Fundamentalsystem für die Tschebyschow-Differentialgleichung. Für ganzzahlige n brechen diese Reihen nach endlich vielen Gliedern ab, und man erhält Polynome als Lösung. Mit der Normierung Tn(1) = 1 werden diese als Tschebyschow-Polynome Tn(x) bezeichnet. Die ersten sieben Polynome dieser Art sind:
Sie können in allgemeiner Weise aus dem rekursiven Zusammenhang
berechnet werden. Mit Hilfe der trigonometrischen Funktionen sind die Tschebyschow-Polynome darstellbar als
oder
Die n Nullstellen des Tschebyschow-Polynoms Tn(x) sind gegeben durch
Anwendungen
In der Filtertechnik werden die Tschebyschow-Polynome bei den Tschebyschow-Filtern verwendet. Bei der Polynominterpolation zeichnen sich diese Polynome durch einen sehr günstigen, gleichmäßigen Fehlerverlauf aus. Dazu sind als Interpolationsstellen die geeignet verschobenen Nullstellen des Tschebyschow-Polynoms passenden Grades zu verwenden. Wegen ihrer Minimalität bilden sie auch die Grundlage für die Tschebyscheff-Iteration und für Fehlerschranken bei Krylow-Unterraum-Verfahren für Lineare Gleichungssysteme.
Wikimedia Foundation.

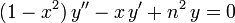
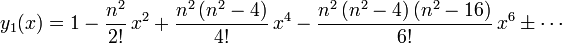
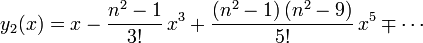
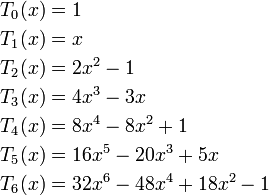
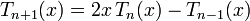
![T_n(x)=\cos\left(n \, \arccos x\right) \quad\mathrm{f\ddot{u}r}\quad x \in [-1,1]](/pictures/dewiki/55/7e606ad5acbdcc1616f29b1b88efcc56.png)