Frequenzgang

Dieser Artikel wurde den Mitarbeitern der Redaktion Physik zur Qualitätssicherung aufgetragen. Wenn Du Dich mit dem Thema auskennst, bist Du herzlich eingeladen, Dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt.

---

Der Frequenzgang beschreibt den Zusammenhang zwischen sinusförmigen Schwingungen am Ein- und Ausgang eines linearen zeitinvarianten Systems (LZI-Systems, Übertragungsglied).^[1]

Gegenüber der Eingangsschwingung hat die Ausgangsschwingung wegen des linearen Verhaltens des Systems dieselbe Frequenz; veränderlich sind seine Amplitude und seine Phase. Das Amplitudenverhältnis und die Phasenverschiebung – je als Funktion der Frequenz f oder Kreisfrequenz ω – sind zusammen der Frequenzgang, einzeln der Amplituden-Frequenzgang und der Phasen-Frequenzgang.

Allgemeines

Bei einem LZI-System beschreibt der Frequenzgang den Zusammenhang zwischen sinusförmigen Schwingungen am Ein- und Ausgang des Übertragungsglieds als Funktion der Frequenz f oder der Kreisfrequenz ω.^[1]

Frequenzantwort eines PT1-Gliedes:
Die Ausgangsamplitude ist bei höherer Frequenz kleiner.

Bode-Diagramm:
Amplituden- und Phasen-Frequenzgang eines passiven Tiefpasses oder PT1-Gliedes

Ortskurve eines passiven Tiefpasses oder PT₁-Glieds

Ein solches System hat bei harmonischem Eingangssignal

$x(t)=\hat x\sin(\omega t + \phi_x)\;$

ein harmonisches Ausgangssignal:

$y(t)=\hat y(\omega) \sin(\omega t+\phi_y(\omega))\;$.

Auf Grund der Linearität wird die Kreisfrequenz $\omega\;$ nicht beeinflusst. Lediglich Amplitude ( $\hat x\;$ → $\hat y\;$ ) und Phase ( $\phi_x\;$ → $\phi_y\;$ ) werden verändert. Amplituden-Frequenzgang ist das Verhältnis

$A(\omega)=\frac{\hat y(\omega)}{\hat x}$.

Phasen-Frequenzgang ist die Phasendifferenz

$\phi(\omega)=\phi_y(\omega)-\phi_x\;$.

Graphische Darstellung

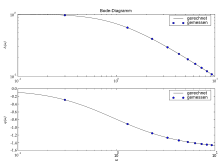
Bode-Diagramm

Zur anschaulichen Darstellung des Frequenzgangs dient das Bode-Diagramm (siehe Abbildung). In je einem Graph ist der Amplituden-Frequenzgang und der Phasen-Frequenzgang dargestellt. Die Achsen sind mehrheitlich logarithmisch geteilt (außer der für die Phasenverschiebung), was den Gebrauch des Diagramms erleichtert. So ist zum Beispiel die Multiplikation zweier Frequenzgänge eine einfache Streckenaddition, und die Inversion eines Frequenzgangs ergibt sich durch Spiegelung an der f- oder ω- Achse im Diagramm.^[2]

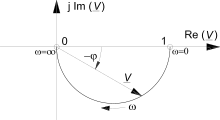
Ortskurve

Eine alternative anschauliche Darstellung des Frequenzgangs ist seine Ortskurve. Dieses Zeigerbild enthält im Gegensatz zum Bode-Diagramm beide Informationen: Die Zeigerlänge entspricht dem Amplitudenverhältnis, sein Argument φ ist die Phasenverschiebung.

Die in der Regelungstechnik verwendete Ortskurve des Frequenzgangs wird auch Nyquist-Diagramm genannt. Mit der Vorstellung, dass in der (komplexen) Ebene lediglich die Spitzen eingefrorener Zeiger, die umlaufend Schwingungen als Kreisbewegungen darstellen, zur Ortskurve verbunden sind, kann der Frequenzgang ohne Kenntnis der komplexen Mathematik und der mathematischen Transformationen aus dem Zeit- in den Frequenzbereich anschaulich gemacht werden.

Fourier-Transformation

LZI-Systeme mit endlich vielen inneren Freiheitsgraden werden durch die lineare Differentialgleichung n-ter Ordnung im Zeitbereich (Zeit als Variable) beschrieben:

$y^{(n)} + a_{n-1}y^{(n-1)} + \ldots + a_{1}y^{(1)} + a_{0}y = b_{m}x^{(m)} + \ldots + b_{1}x^{(1)} + b_{0}x$.

Die Anwendung der Fourier-Transformation auf die Differentialgleichung führt zum Frequenzgang als Bild-Funktion in der komplexen Zahlenebene.

Frequenzgang H(jω) ist der Quotient aus den Fouriertransformierten Y(jω) des Ausgangs-Signals und X(jω) des Eingangs-Signals:

$H(\mathrm j\omega) = \frac{Y(\mathrm j\omega)}{X(\mathrm j\omega)} = \frac{b_{m}(\mathrm j\omega)^{m} + \ldots + b_1(\mathrm j\omega) + b_0}{(\mathrm j\omega)^{n} + a_{n-1}(\mathrm j\omega)^{n-1} + \ldots + a_1(\mathrm j\omega) + a_0}$.

Fourier-Rücktransformierte des Frequenzganges ist die Gewichtsfunktion oder Impulsantwort:

$g(t) =\frac{1}{2\pi}\int_{-\infty}^\infty H(\mathrm j\omega) e^{\mathrm j\omega t} \mathrm d\omega$.

Schreibweisen des Frequenzgangs:

• mit Real- und Imaginärteil

$H(\mathrm j\omega)=\operatorname{Re} H(\mathrm j\omega) + \mathrm j\,\operatorname{Im} H(\mathrm j\omega)$ .

• mit Betrag und Phase

$H(\mathrm j\omega)=\left|H(\mathrm \mathrm j\omega)\right|e^{\mathrm j\varphi(\mathrm j\omega)}$.

$\left|H(\mathrm j\omega)\right| = \sqrt{(\operatorname{Re} H(\mathrm j\omega))^2 + (\operatorname{Im} H(\mathrm j\omega))^2}$     Betrag

$\varphi(\mathrm j\omega) = \arctan\left(\frac{\operatorname{Im} H(\mathrm j\omega)}{\operatorname{Re} H(\mathrm j\omega)}\right)$     Phase

Zusammenhang mit der Übertragungsfunktion

→ Hauptartikel: Übertragungsfunktion

Die Bedeutung des Frequenzgangs für LZI-Systeme beruht auf der Einfachheit seiner experimentellen Gewinnung (zum Beispiel in der Nachrichtentechnik mittels Wobbelgenerator). Er schließt aber Übergangsvorgänge nicht ein. Bei der theoretischen Behandlung des Systems ist dieser Fall mit der Übertragungsfunktion, die den Frequenzgang einschließt, erfassbar.

Mit σ = 0 in s = σ + jω geht die Übertragungsfunktion in den Frequenzgang über.

Wortbedeutung im weiteren Sinn

In einem allgemeineren Sinn kann mit ‘Frequenzgang’ auch der Verlauf einer physikalischen Größe, wie zum Beispiel einer Strahlungsleistung, als Funktion einer Frequenz gemeint sein.^[3][4] Gebräuchlicher als ‘Frequenzgang einer Strahlungsleistung’ ist allerdings die Ausdrucksweise ‘Frequenzabhängigkeit einer Strahlungsleistung’ oder einfach ‘Strahlungsspektrum’. Einer Quelle zufolge bezeichne ‘Frequenzgang’ im Sprachgebrauch der Regelungstechniker auch das Frequenzspektrum von speziellen nichtperiodischen Anregungssignalen.^[5]

Literatur

• Heinz Unbehauen: Regelungstechnik I. Friedr. Vieweg & Sohn Verlagsgesellschaft mbH, 1997, ISBN 3-528-83332-7.
• Jan Lunze: Regelungstechnik 1. 6 Auflage. Springer Verlag, Berlin 2007, ISBN 978-3-540-70790-5.
• Wilfried Weißgerber: Elektrotechnik für Ingenieure 2. Vieweg, 2007, ISBN 978-3-8348-0191-3.

Einzelnachweise

1. ↑ ^{a b} Otto Föllinger. Über die Begriffe „Übertragungsfunktion“ und „Frequenzgang“. Regelungstechnik, Heft 12, 1969, S. 559–562.
2. ↑ Winfried Oppelt: Kleines Handbuch technischer Regelvorgänge. Verlag Chemie, 1972, ISBN 3-527-25347-5, S. 60.
3. ↑ Bibliographisches Institut & F. A. Brockhaus AG: Die Brockhaus Enzyklopädie-Online, Eintrag abgerufen am 22. Juni 2010. Der einleitende Text definiert den Begriff Frequenzgang folgendermaßen: Physik, Technik: allgemein der Verlauf einer physikalischen Größe als Funktion der Frequenz (der Kreisfrequenz ω), auch Bezeichnung für diese Funktion selbst; im engeren Sinn Bezeichnung für eine komplexe Funktion, die das Zeitverhalten zeitinvarianter linearer Übertragungsglieder der Nachrichten- oder Regelungstechnik kennzeichnet; Internet-Link
4. ↑ Kurt Magnus, Karl Popp: Schwingungen - Eine Einführung in die physikalischen Grundlagen und die theoretische Behandlung von Schwingungsproblemen. Teubner, ISBN 3-519-52301-9, S. 30 (Eingeschränkte Vorschau in der Google Buchsuche).
5. ↑ K. Reinschke: Lineare Regelungs- und Steuerungstheorie, Springer-Verlag, S. 44 (Eingeschränkte Vorschau in der Google Buchsuche)

Weblinks

• Kennen Sie den Frequenzgang des Gehörs?