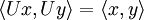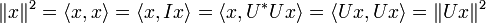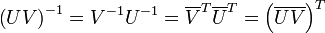Unitären Gruppe

Die unitäre Matrix ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Man bezeichnet damit eine komplexe quadratische Matrix, deren Spalten zueinander orthonormal sind. Dies ist genau dann der Fall, wenn die Matrix U die Gleichung: U ^* U = I erfüllt, wobei I die Einheitsmatrix (Identität) und 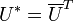$U^* = \overline{U}^T$ die Adjungierte von U ist. Damit gilt für die Inverse einer unitären Matrix

U ^{− 1} = U ^*

Unitäre Matrizen sind das komplexe Analogon zu orthogonalen Matrizen. Bei diesen handelt es sich um unitäre Matrizen, die nur reelle Koeffizienten haben. Während orthogonale Matrizen im allgemeinen nicht diagonalisierbar sind, gilt dies für unitäre allgemein. Die Menge aller unitären Matrizen der Ordnung n bildet die unitäre Gruppe U(n). Die Untergruppe der unitären Matrizen mit Determinante 1 heißt spezielle unitäre Gruppe SU(n).

Unitäre Matrizen sind die Darstellungsmatrizen unitärer Abbildungen. Diese sind längen- und winkeltreu und lassen damit insbesondere das Skalarprodukt invariant:

$\langle U{x},U{y}\rangle=\langle x,y\rangle$

denn es gilt

$\|x\|^2 = \langle x,x \rangle = \langle x,Ix\rangle = \langle x,U^* U x\rangle = \langle Ux,Ux\rangle = \|Ux\|^2$

Daraus folgt, dass alle Eigenwerte unitärer Matrizen den Betrag 1 haben: Sei λ ein Eigenwert und 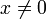${x}\neq{0}$ ein dazugehöriger Eigenvektor, also Ux = λx. Dann gilt

$\langle{x},{x}\rangle = \langle U{x},U{x}\rangle = \langle\lambda{x},\lambda{x}\rangle = \lambda\overline{\lambda}\langle{x},{x}\rangle$,

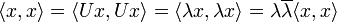Division durch 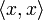$\langle{x},{x}\rangle$ liefert | λ | = 1.

Die Determinante einer unitären Matrix hat ebenfalls den Betrag 1, denn

$1 = \det(I) = \det(UU^*) = \det(U) \cdot \det(U^*) = \det(U) \cdot \det(\overline{U}^T) = \det(U) \cdot \det(\overline{U}) = \det(U) \cdot \overline{\det(U)}= |\det(U)|^2$

Das Produkt zweier unitärer Matrizen ist wieder unitär:

$\left(UV\right)^{-1}= V^{-1} U^{-1}=\overline{V}^{T}\overline{U}^{T}=\left(\overline{UV}\right)^{ T}$

Ist U eine unitäre und A eine idempotente Matrix, also AA = A, so ist B = UAU ^* ebenfalls idempotent:

BB = UAU ^* UAU ^* = UAAU ^* = UAU ^* = B