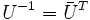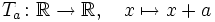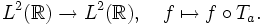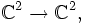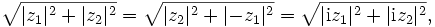- Unitäre Transformation
-
Als unitäre Abbildung (auch unitäre Transformation) bezeichnet man in der Mathematik eine bijektive lineare Abbildung, die längen- und winkelerhaltend ist. Beispiele hierfür sind Drehungen und Spiegelungen. Mathematisch bedeutet dies, dass eine unitäre Abbildung
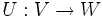 von einem unitären Vektorraum V auf einen anderen unitären Vektorraum W die Norm erhält, dass also für alle
von einem unitären Vektorraum V auf einen anderen unitären Vektorraum W die Norm erhält, dass also für alle 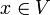 die Bedingung
die Bedingung 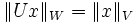 gilt. Sie ist daher eine spezielle Form einer isometrischen Abbildung. Die Normerhaltung ist äquivalent zur Invarianz des Skalarprodukts, d. h.
gilt. Sie ist daher eine spezielle Form einer isometrischen Abbildung. Die Normerhaltung ist äquivalent zur Invarianz des Skalarprodukts, d. h. 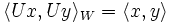 für alle
für alle 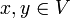 .
.Inhaltsverzeichnis
Endlichdimensionale Vektorräume
Unitäre Abbildungen bezüglich des Standardskalarprodukts auf dem
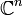 werden durch unitäre Matrizen beschrieben. Unitarität ist dort als
werden durch unitäre Matrizen beschrieben. Unitarität ist dort alsdefiniert, wobei
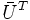 die sogenannte adjungierte Matrix zu U ist, die durch Transposition (Vertauschen von Zeilen und Spalten) sowie komplexe Konjugation der Einträge von U entsteht.
die sogenannte adjungierte Matrix zu U ist, die durch Transposition (Vertauschen von Zeilen und Spalten) sowie komplexe Konjugation der Einträge von U entsteht.Eine andere Charakterisierung ist die folgende: Eine Abbildung ist genau dann unitär, wenn sie
- als Abbildung zwischen den zugrundeliegenden reellen Vektorräumen orthogonal ist (man beachte, dass die reelle Dimension der Vektorräume doppelt so groß ist wie ihre komplexe Dimension)
- und mit der Multiplikation mit der imaginären Einheit i kommutiert.
Unendlichdimensionale Vektorräume
In unendlichdimensionalen Hilberträumen lassen sich lineare Abbildungen nicht durch Matrizen darstellen. Hier ist die Unitarität einer linearen Abbildung φ durch die Bedingung
- φ * = φ − 1
definiert, wobei φ * die adjungierte Abbildung zu φ ist.
Darstellung mit selbstadjungierten Operatoren
Im zuletzt genannten Fall gilt aber folgende Darstellung mit selbstadjungierten Operatoren (Stonescher Satz):
Es sei
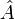 ein selbstadjungierter Operator, welcher im Intervall
ein selbstadjungierter Operator, welcher im Intervall ![s\in [s_0,s]](/pictures/dewiki/57/9a7107482bbab1cbf54f19400170d500.png) nicht vom Parameter s abhänge. Dann ist die Operatorschar
nicht vom Parameter s abhänge. Dann ist die Operatorschar 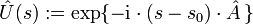 unitär. Auf diese Weise erhält man die Zeitentwicklungsoperatoren der Quantenmechanik; i ist dabei die imaginäre Einheit. Die Operatoren
unitär. Auf diese Weise erhält man die Zeitentwicklungsoperatoren der Quantenmechanik; i ist dabei die imaginäre Einheit. Die Operatoren 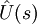 können dabei auf dem ganzen Hilbertraum definiert werden, obwohl
können dabei auf dem ganzen Hilbertraum definiert werden, obwohl 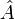 nur dicht-definiert sein muss.
nur dicht-definiert sein muss.Bei Parameterabhängigkeit von
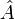 (in der Quantenmechanik z. B. bei expliziter Zeitabhängigkeit des Hamiltonoperators) gilt eine formal ähnliche Aussage (Dyson-Entwicklung):
(in der Quantenmechanik z. B. bei expliziter Zeitabhängigkeit des Hamiltonoperators) gilt eine formal ähnliche Aussage (Dyson-Entwicklung):Zunächst stellt man die Differentialgleichung
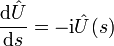 auf und löst sie iterativ durch folgende formale Reihe:
auf und löst sie iterativ durch folgende formale Reihe: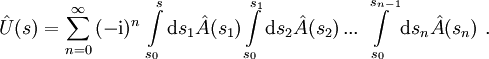
Jetzt kann man durch Permutation der Argumente die oberen Integrationsgrenzen einheitlich auf den Wert s erhöhen (z. B.
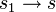 ), wenn man die dadurch erfolgte Ausdehnung des Integrationsgebietes durch einen Faktor 1 / n! kompensiert und für die Einhaltung der Integrationsordnung sorgt (erstes Integrationsargument größer als das zweite, zweites größer als das dritte, u.s.w.). Auf diese Weise erhält man mit dem Dysonschen Integrationsordnungoperator
), wenn man die dadurch erfolgte Ausdehnung des Integrationsgebietes durch einen Faktor 1 / n! kompensiert und für die Einhaltung der Integrationsordnung sorgt (erstes Integrationsargument größer als das zweite, zweites größer als das dritte, u.s.w.). Auf diese Weise erhält man mit dem Dysonschen Integrationsordnungoperator 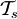 die suggestive Formel, dass die folgende Operatorschar unitär ist:
die suggestive Formel, dass die folgende Operatorschar unitär ist: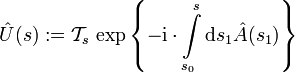
Beispiele
- Auf dem Hilbertraum
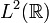 induzieren die Translationen
induzieren die Translationen
-
- für beliebige
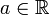 unitäre Operatoren
unitäre Operatoren
- Die im
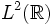 definierte Fourier-Transformation.
definierte Fourier-Transformation. - Ein wichtiges Beispiel für unitäre Transformationen sind die Zeitentwicklungsoperatoren der Quantenmechanik.
Zahlenbeispiel für den endlichdimensionalen Fall
Einfache Beispiele für unitäre Abbildungen sind die lineare Abbildungen A bzw. B
die durch die Matrizen
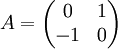 bzw.
bzw. 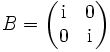
gegeben sind. Explizit sind sie gegeben durch
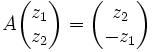 und
und 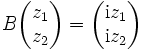 .
.
Die Abbildungen erhalten die Norm
und die zugehörigen Matrizen sind unitär:
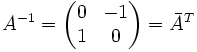 und
und 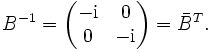
Wikimedia Foundation.