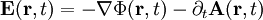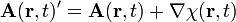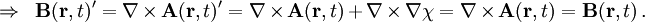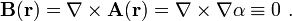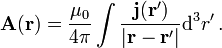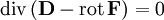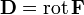- Vektorpozential
-
In der klassischen Elektrodynamik, einem Teilgebiet der Physik, wurde das Vektorpotential
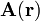 als mathematisches Hilfsmittel eingeführt, um den Umgang mit der magnetischen Induktion
als mathematisches Hilfsmittel eingeführt, um den Umgang mit der magnetischen Induktion 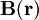 (anschaulich: das "Magnetfeld") zu vereinfachen. Es lässt sich verwenden, um die Maxwell-Gleichungen, welche das elektromagnetische Feld beschreiben, zu entkoppeln und so leichter lösbar zu machen. Es zeigt sich, dass das Vektorpotential über eine Faltung aus einer gegebenen ortsabhängigen Stromdichte
(anschaulich: das "Magnetfeld") zu vereinfachen. Es lässt sich verwenden, um die Maxwell-Gleichungen, welche das elektromagnetische Feld beschreiben, zu entkoppeln und so leichter lösbar zu machen. Es zeigt sich, dass das Vektorpotential über eine Faltung aus einer gegebenen ortsabhängigen Stromdichte 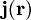 hervorgeht. Man kann also das Vektorpotential zu einer gegebenen Stromdichte berechnen und daraus dann die magnetische Induktion
hervorgeht. Man kann also das Vektorpotential zu einer gegebenen Stromdichte berechnen und daraus dann die magnetische Induktion 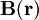 , welche durch diese Verteilung erzeugt wird. Die magnetische Induktion ist (im Gegensatz zum Vektorpotential) eine direkt messbare Größe. Unter einer ortsabhängigen Stromdichte kann man sich etwa eine Anordnung von stromdurchflossenen Leitern im Raum vorstellen, wie einen zu einer Spule gewundenen Draht, oder auch nur einen einzelnen stromdurchflossenen Draht. Der Aharonov-Bohm-Effekt kann über magnetische Induktion nicht erklärt werden, sondern nur über das Vektorpotential, so dass es doch mehr ist, als nur ein mathematisches Hilfsmittel, als das es historisch eingeführt wurde.
, welche durch diese Verteilung erzeugt wird. Die magnetische Induktion ist (im Gegensatz zum Vektorpotential) eine direkt messbare Größe. Unter einer ortsabhängigen Stromdichte kann man sich etwa eine Anordnung von stromdurchflossenen Leitern im Raum vorstellen, wie einen zu einer Spule gewundenen Draht, oder auch nur einen einzelnen stromdurchflossenen Draht. Der Aharonov-Bohm-Effekt kann über magnetische Induktion nicht erklärt werden, sondern nur über das Vektorpotential, so dass es doch mehr ist, als nur ein mathematisches Hilfsmittel, als das es historisch eingeführt wurde.Inhaltsverzeichnis
Definition
Das Vektorpotential
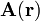 wird so definiert, dass
wird so definiert, dassgilt. Hierbei ist
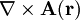 die Rotation des Vektorpotentials. Durch diesen Ansatz ist die Divergenz von
die Rotation des Vektorpotentials. Durch diesen Ansatz ist die Divergenz von 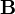 Null, da
Null, da 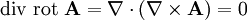 . Dies wird durch die Maxwellgleichungen gefordert.
. Dies wird durch die Maxwellgleichungen gefordert.In der Elektrodynamik gilt die obige Formel unverändert, wohingegen für das elektrische Feld
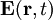
gilt. Hierbei ist Φ das skalare Potential.
Diese beiden Ansätze, zusammen mit der Lorenz-Eichung, werden benutzt, um die Maxwellgleichungen zu entkoppeln. In der Magnetostatik wird für gewöhnlich die Coulomb-Eichung benutzt, die den statischen Grenzfall der Lorenz-Eichung darstellt.
Eigenschaften des Vektorpotentials
(1) Das Vektorpotential ist nur bis auf ein Gradientenfeld bestimmt, weil die Rotation eines Gradientenfeldes immer verschwindet. Für jede skalare Funktion
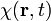 gilt also
gilt also- Verschieden geeichte Vektorpotentiale führen also auf dasselbe magnetische Feld. Dies wird als Eichinvarianz bezeichnet.
(2) Das Vektorpotential ist als Vektorfeld nicht konservativ. Andernfalls wäre es durch den Gradienten eines skalaren Feldes α darstellbar und es würde gelten:
(3) In der Magnetostatik kann das Vektorpotential über die Coulomb-Eichung quellfrei gemacht werden, das bedeutet
-
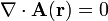 .
.
(4) In der Elektrodynamik, d.h. bei nicht-statischen Verhältnissen, benutzt man dagegen meist die sog. Lorenz-Eichung, nämlich folgende Beziehung, die für die Berechnung elektromagnetischer Wellenfelder nützlich ist:
-
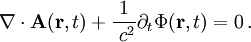 Dabei ist
Dabei ist 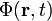 das sog. skalare Potential (s.u.).
das sog. skalare Potential (s.u.).
(5) In der Magnetostatik erfüllt das Vektorpotential die Poisson-Gleichung, für die gilt
-
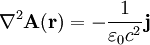 .
.
- Daraus erhält man folgende einfache Darstellung des Vektorpotentials über eine Faltung:
Die Ausdrücke
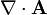 und
und 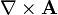 werden manchmal auch als
werden manchmal auch als 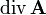 bzw.
bzw. 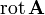 bezeichnet.
bezeichnet.(6) In der Elektrodynamik erweitert sich die Poisson-Gleichung zur (inhomogenen) Wellengleichung für das Vektorpotential
-
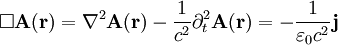 ,
,
- wobei
 der d'Alembert-Operator ist.
der d'Alembert-Operator ist.
Die Lösung dieser Gleichung ist das sog. retardierte Vektorpotential
-
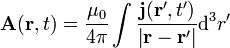 , mit
, mit 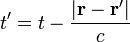 .
.
(7) Die drei Komponenten Ax, Ay und Az des Vektorpotentials und das skalare Potential Φ / c können in der Elektrodynamik zu einem sog. Vierervektor zusammengefasst werden, der sich bei den sog. Lorentz-Transformationen der Speziellen Relativitätstheorie Albert Einsteins wie das Quadrupel (x, y, z ,ct) transformiert. c ist dabei die Vakuum-Lichtgeschwindigkeit.
Elektrisches Vektorpotential
Bei der Berechnung von Feldern in ladungs- und leitungsstromfreien Gebieten, z.B. in Hohlleitern begegnet man dem elektrischen Vektorpotential
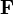 .
.Auf Grund der Quellenfreiheit der betrachteten Felder gilt
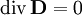 bzw.
bzw.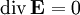 sowie
sowie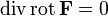 .
.
Um einen funktionalen Zusammenhang zwischen
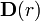 und
und 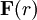 zu erhalten subtrahiert man die Gleichungen
zu erhalten subtrahiert man die Gleichungen 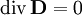 und
und 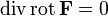 voneinander und erhält:
voneinander und erhält:Daraus folgt dann
Das Vektorfeld
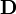 ist also die Wirbeldichte von
ist also die Wirbeldichte von 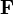 .
.Das Wirbelfeld
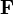 nennt man elektrisches Vektorpotential. Es beschreibt nur zeitlich veränderliche elektrische Felder.
nennt man elektrisches Vektorpotential. Es beschreibt nur zeitlich veränderliche elektrische Felder.Quelle
- Adolf J. Schwab: Begriffswelt der Feldtheorie, Springer Verlag, ISBN 3-540-42018-5
Wikimedia Foundation.