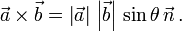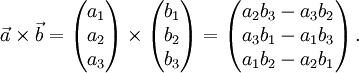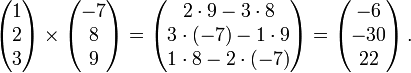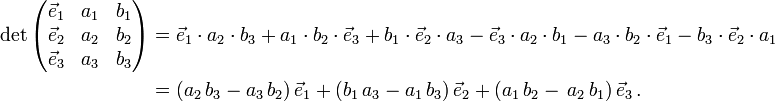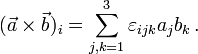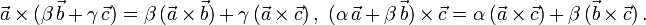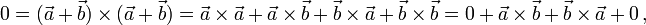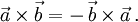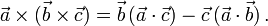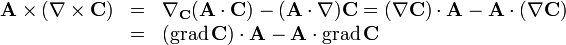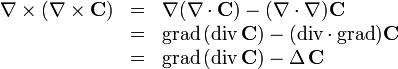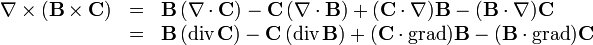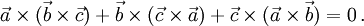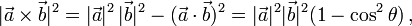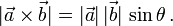- Vektorprodukt
-
Das Kreuzprodukt
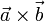 (auch Vektorprodukt, vektorielles Produkt oder äußeres Produkt genannt) zweier Vektoren
(auch Vektorprodukt, vektorielles Produkt oder äußeres Produkt genannt) zweier Vektoren  und
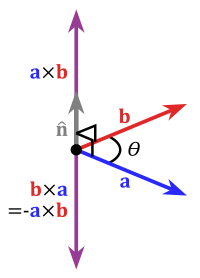
und  im dreidimensionalen reellen Vektorraum ist ein Vektor, der senkrecht auf der von den beiden Vektoren aufgespannten Ebene steht und mit ihnen ein Rechtssystem bildet. Die Länge dieses Vektors ist die Flächengröße des Parallelogramms mit den Seiten
im dreidimensionalen reellen Vektorraum ist ein Vektor, der senkrecht auf der von den beiden Vektoren aufgespannten Ebene steht und mit ihnen ein Rechtssystem bildet. Die Länge dieses Vektors ist die Flächengröße des Parallelogramms mit den Seiten  und
und  .
.Das Kreuzprodukt tritt in der Physik beispielsweise bei der Lorentzkraft oder dem Drehmoment auf.
Das Kreuzprodukt wird mit einem Kreuz als Multiplikationszeichen geschrieben. Es gilt
Dabei sind
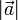 und
und 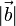 die Längen der Vektoren
die Längen der Vektoren 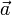 und
und 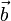 und
und 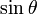 ist der Sinus des von ihnen eingeschlossenen Winkels θ. Der Vektor
ist der Sinus des von ihnen eingeschlossenen Winkels θ. Der Vektor 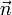 ist der zu
ist der zu 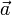 und
und 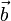 senkrechte Einheitsvektor, der sie zu einem Rechtssystem ergänzt. Das heißt,
senkrechte Einheitsvektor, der sie zu einem Rechtssystem ergänzt. Das heißt, 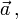
 und
und 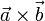 verhalten sich wie Daumen, Zeigefinger und Mittelfinger der rechten Hand (Rechte-Hand-Regel).
verhalten sich wie Daumen, Zeigefinger und Mittelfinger der rechten Hand (Rechte-Hand-Regel).Inhaltsverzeichnis
Komponentenweise Berechnung
Für den euklidischen Raum
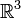 mit der Standardbasis gilt für das Kreuzprodukt:
mit der Standardbasis gilt für das Kreuzprodukt:Ein Zahlenbeispiel:
Das Kreuzprodukt ist symbolisch die Determinante der
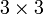 -Matrix, in deren ersten Spalte die Symbole
-Matrix, in deren ersten Spalte die Symbole 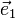 ,
, 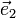 und
und 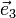 für die kanonische Basis stehen. Die zweite Spalte wird von den Komponenten des Vektors
für die kanonische Basis stehen. Die zweite Spalte wird von den Komponenten des Vektors  und die dritte von denen des Vektors
und die dritte von denen des Vektors  gebildet. Diese Determinante berechnet man nach der Regel von Sarrus:
gebildet. Diese Determinante berechnet man nach der Regel von Sarrus:Mit dem Levi-Civita-Symbol
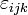 schreiben sich Komponenten als
schreiben sich Komponenten alsBilinearität, Antisymmetrie
Das Kreuzprodukt ist bilinear, für alle Zahlen
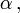 β und γ und alle Vektoren
β und γ und alle Vektoren 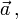
 und
und 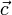 gilt
giltDa die Fläche jedes Parallelogramms verschwindet, das ein Vektor mit sich aufspannt,
ist das Kreuzprodukt antisymmetrisch,
Bei Vertauschung der Vektoren ändert sich also das Vorzeichen. Das Kreuzprodukt ist antikommutativ oder schiefsymmetrisch.
Doppeltes Kreuzprodukt: Graßmann-Identität
Das Kreuzprodukt ist nicht assoziativ. Die Graßmann-Identität (nach Hermann Graßmann), auch Graßmannscher Entwicklungssatz genannt, für das wiederholte Kreuzprodukt von drei Vektoren, deren Komponenten kommutieren, lautet
Sie heißt auch BAC-CAB-Formel, wobei der Name das Ergebnis ausspricht.
Handelt es sich bei den Komponenten der Vektoren um Operatoren oder Matrizen, dann gilt die Formel, falls die Reihenfolge der Operatoren unerheblich ist oder mit der Reihenfolge auf der linken Seite übereinstimmt.
Doppeltes Kreuzprodukt mit Nabla-Operatoren
Ist
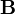 der Nabla-Operator, so lässt sich der Graßmann'sche Entwicklungssatz nicht einfach übertragen, da Nabla stets nach rechts auf
der Nabla-Operator, so lässt sich der Graßmann'sche Entwicklungssatz nicht einfach übertragen, da Nabla stets nach rechts auf 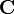 wirkt (Notation im Folgenden:
wirkt (Notation im Folgenden: 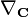 differenziert nur die Komponenten des Vektors
differenziert nur die Komponenten des Vektors 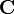 und
und 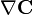 ist der Vektorgradient, also die Jacobi-Matrix von
ist der Vektorgradient, also die Jacobi-Matrix von 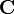 ):
):Daher gilt, falls
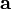 und
und 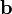 der Nabla-Operator und
der Nabla-Operator und 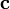 ein Vektorfeld ist, in der Form:
ein Vektorfeld ist, in der Form:Für die Rotation des Kreuzprodukts zweier Vektorfelder
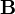 und
und 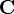 gilt hingegen:
gilt hingegen:Die zusätzlichen Terme entstehen, weil die Ableitung eines Produktes nach der Produktregel zwei Terme ergibt.
Jacobi-Identität
Wenn die Komponenten der Vektoren kommutieren, gilt die Jacobi-Identität, dass die zyklische Summe wiederholter Kreuzprodukte verschwindet,
Lagrange-Identität
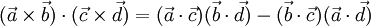 .
.
Für das Quadrat der Norm erhält man hieraus
also ist der Betrag des Kreuzproduktes
Zusammenhang mit Lie-Algebra
Für einen Körper
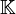 bildet der
bildet der 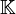 -Vektorraum
-Vektorraum 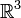 zusammen mit dem Kreuzprodukt eine Lie-Algebra.
zusammen mit dem Kreuzprodukt eine Lie-Algebra.Kreuzprodukt im

Das Kreuzprodukt aus zwei gewöhnlichen (polaren)
 Vektoren liefert einen sogenannten axialen Vektor. Streng genommen handelt es sich um einen Tensor zweiter Stufe mit drei unabhängigen Komponenten:
Vektoren liefert einen sogenannten axialen Vektor. Streng genommen handelt es sich um einen Tensor zweiter Stufe mit drei unabhängigen Komponenten: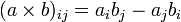
Mit dieser Definition lässt sich der Tensor auch für Vektorräume n > 3 definieren. Im
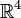 hat das Kreuzprodukt beispielsweise 6 unabhängige Elemente. Sie lassen sich nicht mehr als
hat das Kreuzprodukt beispielsweise 6 unabhängige Elemente. Sie lassen sich nicht mehr als 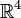 -Vektor darstellen[1]
-Vektor darstellen[1]Siehe auch
Einzelnachweise
- ↑ http://folk.uio.no/patricg/teaching/a112/levi-civita/ Levi-Civita symbol and cross product vector/tensor
Weblinks
- Java-Applet der Universität von Syracuse zum Vektor- oder Kreuzprodukt
Wikimedia Foundation.