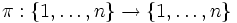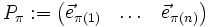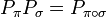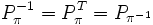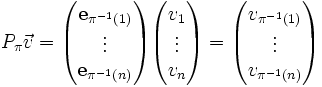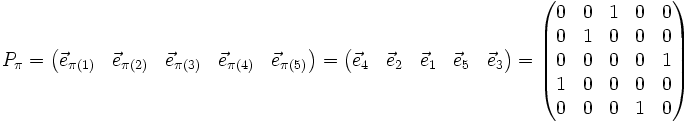Vertauschungsmatrix

Unter einer Permutationsmatrix oder auch Vertauschungsmatrix versteht man eine binäre Matrix (eine Matrix die nur 0- und 1-Einträge hat), die in jeder Zeile und in jeder Spalte genau einen 1-Eintrag hat. Diese Matrizen repräsentieren Permutationen auf Vektoren.

Definition

Ist eine Permutation π von n Elementen gegeben:

$\pi : \lbrace 1, \dots, n \rbrace \to \lbrace 1, \dots, n \rbrace$

So ist die Permutionsmatrix P_π wie folgt definiert:

$P_{\pi} := \begin{pmatrix} \vec{e}_{\pi(1)}& \dots& \vec{e}_{\pi(n)} \end{pmatrix}$

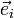wobei $\vec{e}_i$ der i-te kanonische Basisvektor ist

Eigenschaften

Hat man zwei Permutationen 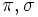$\pi , \sigma \!$ gegeben dann gilt folgende Beziehung zwischen den Permutationsmatrizen:

$P_{\pi} P_{\sigma} = P_{\pi \circ \sigma}$

Permutationsmatrizen sind orthogonale Matrizen, daher existiert eine eindeutige Inverse und es gilt:

$P_{\pi}^{-1} = P_{\pi}^{T} = P_{\pi^{-1}}$

Multipliziert man eine Permutationsmatrix 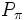$P_{\pi}\!$ mit einem Vektor so werden die Einträge des Vektors permutiert

$P_\pi \vec{v} = \begin{pmatrix} \mathbf{e}_{\pi^{-1}(1)} \\ \vdots \\ \mathbf{e}_{\pi^{-1}(n)} \end{pmatrix} \begin{pmatrix} v_1 \\ \vdots \\ v_n \end{pmatrix} = \begin{pmatrix} v_{\pi^{-1}(1)} \\ \vdots \\ v_{\pi^{-1}(n)} \end{pmatrix}$

Weitere Eigenschaften

• Eine Permutionsmatrix ist eine Stochastische Matrix.
• Permutationsmatrizen können als Produkt von elementaren (zeilenvertauschenden) Matrizen dargestellt werden.
• Die Spur einer Permutationsmatrix entspricht der Anzahl der Fixpunkte der Permutation.
• Die Determinante einer Permutationsmatrix entspricht dem Signum der Permutation.
• Die Menge der Permutationsmatrizen bildet auf 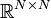$\mathbb{R}^{N\times N}$ zusammen mit der Matrizenmultiplikation eine Gruppe.

Beispiele

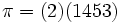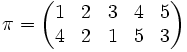Sei eine Permutation $\pi =(2)(1 4 5 3)\!$ bzw. $\pi = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 2 & 1 & 5 & 3 \\ \end{pmatrix}$ gegeben.

Die zugehörige Permutationsmatrix hat nun folgende Form:

$P_{\pi} = \begin{pmatrix} \vec{e}_{\pi(1)}& \vec{e}_{\pi(2)}& \vec{e}_{\pi(3)}& \vec{e}_{\pi(4)}& \vec{e}_{\pi(5)} \end{pmatrix} = \begin{pmatrix} \vec{e}_4 & \vec{e}_2 & \vec{e}_1 & \vec{e}_5 & \vec{e}_3 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{pmatrix}$

Hat man nun noch einen Vektor 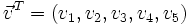$\vec{v}^T = (v_1,v_2,v_3,v_4,v_5)$ gegeben dann gilt:

$P_{\pi} \vec{v} = \begin{pmatrix} 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \end{pmatrix} = \begin{pmatrix} v_3 \\ v_2 \\ v_5 \\ v_1 \\ v_4 \end{pmatrix}$