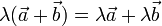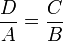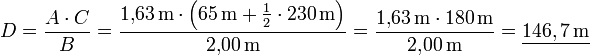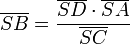- Vierstreckensatz
-
Der Strahlensatz (man spricht auch vom ersten, zweiten und dritten Strahlensatz) oder Vierstreckensatz gehört zu den wichtigsten Aussagen der Elementargeometrie. Er befasst sich mit Streckenverhältnissen und ermöglicht es bei vielen geometrischen Überlegungen, unbekannte Streckenlängen auszurechnen.
Inhaltsverzeichnis
Formulierung der Strahlensätze
Wenn zwei durch einen Punkt (Scheitel) verlaufende Halbgeraden (Strahlen) von zwei parallelen Geraden geschnitten werden, die nicht durch den Scheitel gehen, dann gelten die folgenden Aussagen:
- Es verhalten sich je zwei Abschnitte auf dem einen Strahl zueinander so wie die ihnen entsprechenden Abschnitte auf dem anderen Strahl.
- Es verhalten sich die ausgeschnittenen Strecken auf den Parallelen, wie die ihnen entsprechenden, vom Scheitel aus gemessenen Strecken auf den Strahlen.
- Es stehen je zwei Abschnitte auf den Parallelen, die einander entsprechen, in gleichem Verhältnis zueinander. Dieser Strahlensatz setzt im Gegensatz zu den ersten beiden Strahlensätzen mindestens drei Strahlen voraus. Er ist hier nicht skizziert.
Der erste Strahlensatz bezieht sich also auf die Verhältnisse von Strahlenabschnitten, der zweite auf die Verhältnisse von Strahlen- und Parallelenabschnitten und der dritte auf die Verhältnisse von Parallelenabschnitten.
Bemerkung (Umkehrung des Strahlensatzes): Ist Eigenschaft 1 erfüllt, so kann man auf parallele Geraden schließen. Ist dagegen Eigenschaft 2 gegeben, so ist ein entsprechender Schluss auf Parallelität nicht möglich.
Verwandte geometrische Konzepte
Der Strahlensatz steht in engem Zusammenhang mit dem Begriff der geometrischen Ähnlichkeit. Die Dreiecke ZAB und ZA'B' sind in beiden Skizzen zueinander ähnlich. Dies bedeutet insbesondere, dass entsprechende Seitenverhältnisse in diesen Dreiecken übereinstimmen – eine Aussage, aus der sich unmittelbar der Strahlensatz ergibt.
- Siehe auch: Ähnlichkeitssätze
Ein weiteres Konzept, das mit dem Strahlensatz zusammenhängt, ist das der zentrischen Streckung (einer speziellen geometrischen Abbildung). In der linken Skizze bildet beispielsweise die zentrische Streckung mit Zentrum Z und Streckungsfaktor (Abbildungsfaktor) 1,5 die Punkte A und B auf die Punkte A' bzw. B' ab. Entsprechendes gilt für die rechte Skizze; hier ist der Streckungsfaktor gleich -0,5.
Eine ähnlich enge Beziehung besteht zur Vektorrechnung. Die Rechenregel
für zwei Vektoren
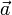 ,
, 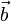 und einen reellen Skalar λ ist nur eine andere Ausdrucksweise für den Strahlensatz.
und einen reellen Skalar λ ist nur eine andere Ausdrucksweise für den Strahlensatz.Einfaches Anwendungsbeispiel
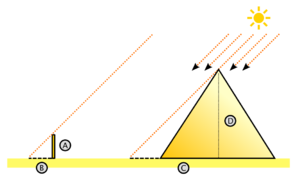
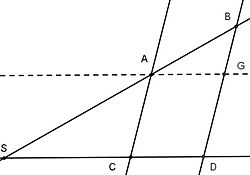
Ein einfaches Beispiel für die Anwendung des Strahlensatzes soll auf den antiken griechischen Philosophen und Mathematiker Thales von Milet zurückgehen. Dieser habe mit Hilfe eines Stabes durch Messung der Schattenlänge die Höhe der ägyptischen Cheopspyramide ermittelt. In der französischsprachigen Literatur wird der Strahlensatz daher auch Théorème de Thalès genannt.
Die folgende Beispielrechnung ermittelt die Höhe der Cheopspyramide mit Hilfe des Strahlensatzes, sie entspricht jedoch vermutlich nicht exakten der Berechnung des Thales selbst[1]:
- Zunächst bestimmte er die Seitenlänge der Pyramide und anschließend die Länge des Schattens eben jener. Anschließend steckte er einen Stab senkrecht in den Boden und vermaß dessen Höhe und dessen Schattenlänge. Dabei ermittelte er folgende Werte:
-
- Höhe des Stabes:
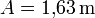
- Schattenlänge des Stabes:
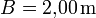
- Schattenlänge der Pyramide:
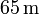
- Seitenlänge der Pyramide:
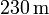
- Höhe des Stabes:
- Mit Hilfe des Strahlensatzes (Skizze 2) stellte er die folgende Gleichung auf:
- Die Länge der Seite C des Dreiecks setzt sich dabei aus der halben Seitenlänge und der Länge des Schattens der Pyramide zusammen. Umgestellt nach D erhielt er:
- So konnte er die Höhe der Cheopspyramide zu
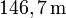 sehr genau bestimmen.
sehr genau bestimmen.
Beweis
Satz 1
Die Lote von D bzw. B auf die durch
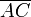 definierte Gerade haben die gleiche Länge, da
definierte Gerade haben die gleiche Länge, da 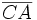 parallel zu
parallel zu 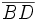 ist. Diese nicht einskizzierten Lote sind Höhen der Dreiecke CDA bzw. CBA, welche die zugehörige Basislinie
ist. Diese nicht einskizzierten Lote sind Höhen der Dreiecke CDA bzw. CBA, welche die zugehörige Basislinie 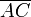 gemeinsam haben. Für die Flächen gilt daher
gemeinsam haben. Für die Flächen gilt daher 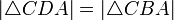 und weiter
und weiter  oder flächenvereint
oder flächenvereint 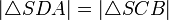 .
.Somit gilt dann auch:
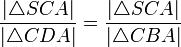 und
und 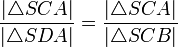
Das Anwenden der Standardformel zur Flächenberechnung von Dreiecken (
 ) liefert dann
) liefert dann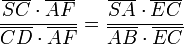 und
und 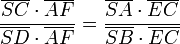
Kürzen liefert
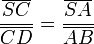 und
und  .
.Löst man beides nach
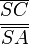 auf und setzt die rechten Seiten gleich ergibt sich :
auf und setzt die rechten Seiten gleich ergibt sich :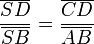
oder umgeformt für die Streckenverhältnisse auf je einem Strahl:
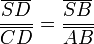 .
.
Satz 1 – Beweis nach Archimedes
Außer des oben angegebenen Beweises, der auf eine Darstellung aus Euklids Elementen (6. Buch, L.2) zurückgeht, waren in der griechischen Antike schon kürzere und elegantere Beweise möglich. Es reicht, die Gleichheit für einen Fall der möglichen Verhältnisse zu zeigen. Die anderen ergeben sich daraus unmittelbar. Euklid selbst beweist auch nur einen Fall.
Hier wird der Beweis nicht zitiert, sondern lediglich gemäß der Archimedischen Methodenlehre[2] ausgeführt:
Mit den üblichen Seiten- und Winkelbezeichnungen für die Dreiecke ABZ und A'B'Z entsprechend der Skizze oben (zur Formulierung der Strahlensätze) wird gezeigt, dass a:a' = b:b' gilt. Die Winkel α und α' sowie β und β' sind als Stufenwinkel gleich. Bezeichne die Höhen, die durch das Lot von Z auf die Geraden gegeben sind, mit h und h' und deren Fußpunkte mit H und H'. Da α gleich α' haben 'ferne' Kathete und Hypotenuse in den beiden rechtwinkligen Dreiecken AHZ und A'H'Z dasselbe Verhältnis zueinander. (In 'moderner' Formulierung: sin(α) gleich Gegenkathete von α zu Hypotenuse)
Also h:b = h':b' und daher h:h' = b:b'.
Aus β gleich β' folgt durch entsprechende Betrachtung der Dreiecke HBZ und H'B'Z die Gleichung h:a = h':a' bzw h:h' = a:a'. Und schließlich a:a' = b:b'. Was zu beweisen war.
Satz 2
Konstruiere eine zusätzliche Parallele zu
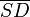 durch A. Diese Parallele schneidet
durch A. Diese Parallele schneidet 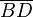 in G. Somit gilt nach Konstruktion
in G. Somit gilt nach Konstruktion 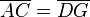 und wegen Satz 1 gilt für die Strahlen durch B außerdem
und wegen Satz 1 gilt für die Strahlen durch B außerdem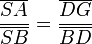 worin sich
worin sich  durch
durch 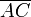 ersetzen lässt:
ersetzen lässt: 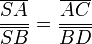
Umkehrung von Satz 1
Vorausgesetzt
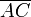 und
und 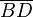 wären nicht parallel. Dann gibt es eine Parallele zu
wären nicht parallel. Dann gibt es eine Parallele zu 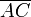 , die durch den Punkt D geht und die Strecke
, die durch den Punkt D geht und die Strecke 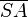 in
in 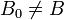 (*) schneidet. Da nach Voraussetzung
(*) schneidet. Da nach Voraussetzung 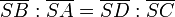 gilt, ergibt sich
gilt, ergibt sichAndererseits gilt nach dem ersten Strahlensatz auch
 .
.
Dies bedeutet, dass B und B0 beide auf dem Strahl
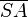 liegen und den gleichen Abstand von S haben. Damit sind die beiden Punkte jedoch identisch, also B = B0. Dies ist ein Widerspruch dazu, dass es sich nach Bedingung (*) um 2 verschiedene Punkte handeln soll. Also führt die Annahme der Nichtparallelität zu einem Widerspruch und kann daher nicht richtig sein; oder anders ausgedrückt: Es muss
liegen und den gleichen Abstand von S haben. Damit sind die beiden Punkte jedoch identisch, also B = B0. Dies ist ein Widerspruch dazu, dass es sich nach Bedingung (*) um 2 verschiedene Punkte handeln soll. Also führt die Annahme der Nichtparallelität zu einem Widerspruch und kann daher nicht richtig sein; oder anders ausgedrückt: Es muss 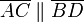 liegen.
liegen.Literatur
- H. Schupp: Elementargeometrie. UTB Schöningh 1977, ISBN 3-506-99189-2, S.124ff
Siehe auch
- Daumensprung, Schätzen der Entfernung nach dem Strahlensatz mittels des eigenen Daumens
Einzelnachweise
- ↑ Von Thales selbst sind keine Werke erhalten geblieben. Es gibt jedoch mehrere historische Quellen, die die Berechnung der Pyramidenhöhe durch Thales erwähnen. Alle diese Quellen sind aber mehrere Jahrhunderte nach dem Tode Thales verfasst worden und leicht unterschiedlich in ihrer Beschreibung, so dass sich letztendlich nicht mit Bestimmtheit sagen lässt, inwieweit Thales den Strahlensatz selbst oder einen Spezialfall von ihm als geometrischen Lehrsatz kannte oder ob er lediglich eine physikalische Beobachtung anwandte. So steht bei Diogenes Laertius: "Hieronymus sagt, dass es Thales sogar gelang die Höhe der Pyramiden zu bestimmen, indem er den Schatten der Pyramide genau in dem Augenblick vermass, in dem sein eigene Schattenlänge seiner Körpergröße entsprach.". Eine ähnliche Formulierung findet man bei Plinius:"Thales entdeckte, wie man die Höhe von Pyramiden und anderen Objekten bestimmt, nämlich indem man den Schatten des Objektes genau zu dem Zeitpunkt misst, an dem Höhe und Schatten gleich lang sind.". Bei Plutarch jedoch findet sich eine Beschreibung, die eventuell eine Kenntnis des Strahlensatzes vermuten lässt:"..ohne Schwierigkeiten und Zuhilfnenahme eines Instrumentes, stellte er lediglich einen Stock am Ende des Pyramidenschatten auf und erhielt so zwei durch die Sonnenstrahlen erzeugte Dreiecke .... dann zeigte er, dass die Höhe des Stocks und die Höhe der Pyramide imselben Verhältnis stehen, wie die Schattenlänge des Stockes und die Schattenlänge der Pyramide" (Quelle: Biographie des Thales im MacTutor)
- ↑ Archimedes Werke. Übersetzt und mit Anmerkungen versehen von Arthur Czwalina Wiss. Buchgesellschaft, Darmstadt 1983, ISBN 3-534-02029-4
Wikimedia Foundation.