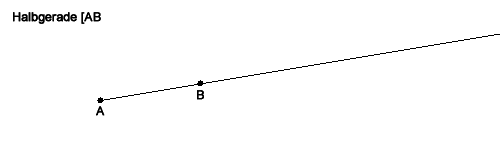
Halbgerade

Der Strahl und die Halbgerade sind in der Geometrie - anschaulich gesprochen - eine gerade Linie, die auf einer Seite begrenzt ist, sich aber auf der anderen Seite ins Unendliche erstreckt.

• Die Halbgerade ist ein geometrisches Objekt, das entsteht, wenn ein Punkt eine Gerade, auf der er liegt, teilt. Dabei ist der Punkt wahlweise Teil der Halbgerade oder nicht.
• Der Strahl verfügt über eine Orientierung: Er geht von einem Anfangspunkt aus.

Strahlen und Halbgeraden müssen demnach unterschieden werden von Geraden, die beidseitig unbegrenzt sind, und von Strecken, die auf beiden Seiten begrenzt sind.

Geometrische Darstellung

Die in der Skizze verwendete Schreibweise [AB drückt aus, dass es sich um eine Teilmenge der Geraden AB handelt, die durch den Punkt A begrenzt wird, sich aber über den Punkt B hinaus erstreckt.

Mit Hilfe der Zwischen-Relation ("... liegt zwischen ... und ...") lässt sich die Halbgerade [AB definieren als die Menge aller Punkte X auf der Geraden AB, für die A nicht zwischen B und X liegt.

Betrachtet man eine Gerade g und einen beliebigen Punkt P auf g, so lassen sich die beiden dadurch festgelegten Strahlen (Halbgeraden) s₁ und s₂ charakterisieren als nicht leere Teilmengen von g, die folgende Bedingungen erfüllen:

• Jeder Punkt auf der Geraden g, der nicht mit P übereinstimmt, gehört zu genau einer der beiden Teilmengen s₁ oder s₂.
• Ist P₁ ein beliebiger Punkt von s₁ und P₂ ein beliebiger Punkt von s₂, so liegt P zwischen P₁ und P₂.

Damit ist die Halbgerade eng mit dem Begriff Intervall verbunden: Ein Intervall lässt sich als Schnittmenge zweier Halbgeraden definieren.

Analytische Darstellung

In der analytischen Geometrie entspricht die Halbgerade [AB der Menge aller Punkte X, deren Ortsvektor 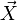$\vec{X}$ gegeben ist durch

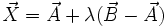$\vec{X} = \vec{A} + \lambda (\vec{B} - \vec{A})$ mit $\lambda \ge 0$.

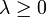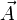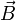Dabei sind $\vec{A}$ und $\vec{B}$ die Ortsvektoren der Endpunkte A und B. λ ist der (reelle) Parameter dieser Parametergleichung.

Siehe auch

• Geordnete Geometrie