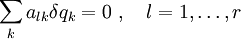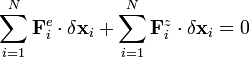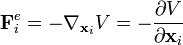Virtuelle Verrückung

Virtuelle Arbeit ist ein Begriff der Analytischen Mechanik bzw. der Technischen Mechanik und bezeichnet die Arbeit, die die eingeprägten Kräfte an einem System bei einer virtuellen Verrückung leisten. Unter einer virtuellen Verrückung versteht man eine Gestalt- oder Lageänderung des Systems, die mit den Bindungen (z. B. Lager) verträglich, sonst aber willkürlich und außerdem infinitesimal klein ist. Nach dem Prinzip der virtuellen Arbeit verschwindet die virtuelle Arbeit in statischen Systemen.

Beschreibung

Im Folgenden wird ein N-Teilchensystem betrachtet, das durch Zwangsbedingungen eingeschränkt ist.

Virtuelle Verrückung, virtuelle Arbeit

Eine virtuelle Verrückung $\delta\mathbf{x}_{i}$ ist eine infinitesimale Verschiebung des i-ten Teilchens, die zeitlos dt = 0 bzw. zu festgehaltener Zeit t=const abläuft (eine reale Verschiebung würde die Zeit dt > 0 benötigen) und mit den gegebenen Zwangsbedingungen verträglich ist. Während einer virtuellen Verrückung ändern sich Zwangsbedingungen und äußere Kräfte, auch wenn diese zeitabhängig sind, nicht, da während dieser virtuellen Verrückung keine Zeit vergeht.

Die s holonomen Zwangsbedingungen werden durch Verwendung von n = 3N − s generalisierten Koordinaten erfüllt:

$\delta\mathbf{x}_{i}=\sum_{k=1}^{n}\frac{\partial\mathbf{x}_{i}}{\partial q_{k}}\delta q_{k}$

Zur Erfüllung der anholonomen Zwangsbedingungen unterliegen die δq_k weiteren Bedingungen, z.B. r differentielle nicht-integrable Gleichungen:

$\,\sum_{k}a_{lk}\delta q_{k}=0\ ,\quad l=1,\ldots,r$

Die virtuelle Arbeit, die die Kraft $\mathbf{F}_{i}$ bei virtueller Verrückung $\delta\mathbf{x}_{i}$ am i-ten Teilchen verrichtet, ist:

$\delta W_{i}=\mathbf{F}_{i}\cdot\delta\mathbf{x}_{i}$

System im Gleichgewicht

Ist das N-Teilchensystem im Gleichgewicht, so ist für jedes Teilchen die Beschleunigung gleich Null:

$\ddot{\mathbf{x}}_{i}=0$

Daher muss die resultierende Kraft auf jedes Teilchen gleich Null sein:

$\mathbf{F}_{i}=m_{i}\ddot{\mathbf{x}}_{i}=0$

Ist das System im Gleichgewicht ist die virtuelle Arbeit der Kraft $\mathbf{F}_{i}$ bei Verrückung $\delta\mathbf{x}_{i}$ gleich Null, da die Kraft selbst verschwindet:

$\delta W_{i}=\mathbf{F}_{i}\cdot\delta\mathbf{x}_{i}=0$

Somit ist auch die Summe über die von allen Kräften bei virtuellen Verrückungen geleistete Arbeit gleich Null:

$\sum_{i=1}^{N}\mathbf{F}_{i}\cdot\delta\mathbf{x}_{i}=0$

Die resultierenden Kräfte $\mathbf{F}_{i}$ kann man zusammensetzen aus eingeprägten Kräften $\mathbf{F}_{i}^{e}$ und Zwangskräften $\mathbf{F}_{i}^{z}$:

$\mathbf{F}_{i}=\mathbf{F}_{i}^{e}+\mathbf{F}_{i}^{z}$

Eingesetzt in obige Beziehung:

$\sum_{i=1}^{N}\mathbf{F}_{i}^{e}\cdot\delta\mathbf{x}_{i}+\sum_{i=1}^{N}\mathbf{F}_{i}^{z}\cdot\delta\mathbf{x}_{i}=0$

Prinzip der virtuellen Arbeit

Meist steht die Zwangskraft $\mathbf{F}_{i}^{z}$ senkrecht zur virtuellen Verrückung $\delta\mathbf{x}_{i}$, so dass $\mathbf{F}_{i}^{z}\cdot\delta\mathbf{x}_{i}=0$ gilt. Dies ist z.B. der Fall, wenn die Bewegung auf Kurven oder Flächen begrenzt ist.

Es gibt allerdings Systeme, bei denen einzelne Zwangskräfte Arbeit verrichten $\mathbf{F}_{i}^{z}\cdot\delta\mathbf{x}_{i}\neq0$.

Das Prinzip der virtuellen Arbeit fordert nun, dass die Summe aller von den Zwangskräften verrichteten virtuellen Arbeiten bei einem System im Gleichgewicht verschwindet:

$\sum_{i=1}^{N}\mathbf{F}_{i}^{z}\cdot\delta\mathbf{x}_{i}=0$

Für die eingeprägten Kräfte bedeutet das Prinzip der virtuellen Arbeit:

$\sum_{i=1}^{N}\mathbf{F}_{i}^{e}\cdot\delta\mathbf{x}_{i}=0$

Man beachte, dass das Prinzip der virtuellen Arbeit nur ein Gleichgewichtsprinzip der Statik ist. Die Erweiterung auf die Dynamik liefert das d’Alembertsches Prinzip.

Prinzip der virtuellen Arbeit in konservativen Systemen

In konservativen Systemen sind alle eingeprägten Kräfte von einem Potential V ableitbar:

$\mathbf{F}_{i}^{e}=-\nabla_{\mathbf{x}_{i}}V=-\frac{\partial V}{\partial\mathbf{x}_{i}}$

In diesem Fall lässt sich das Prinzip der virtuellen Arbeit

$\sum_{i=1}^{N}\mathbf{F}_{i}^{e}\cdot\delta\mathbf{x}_{i}=-\sum_{i=1}^{N}\frac{\partial V}{\partial\mathbf{x}_{i}}\cdot\delta\mathbf{x}_{i}=0$

in der Form

$\delta\, V=0$

darstellen. Hierbei ist das Symbol δ als Variationszeichen im Sinne der Variationsrechnung aufzufassen. δV = 0 bedeutet damit die erste Variation der Potentiellen Energie.

Beispiel

Gelenkig gelagerter Winkelhebel, die virtuelle Verrückung ist durch den Drehwinkel δΦ charakterisiert.

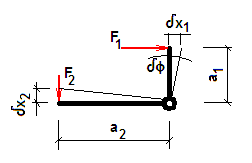
An einem Winkelhebel, der auf einer Achse frei drehbar gelagert ist, greifen 2 eingeprägte Kräfte F₁ und F₂ an. Die virtuellen Verschiebungen der Kraftangriffspunkte sind δx₁ und δx₂. Die virtuelle Arbeit der eingeprägten Kräfte ist damit

F₁δx₁ - F₂δx₂ = 0

Weil der Winkelhebel als starr angesehen wird, sind die Größen δx₁ und δx₂ nicht unabhängig voneinander. Ihre Abhängigkeit kann man durch die Variation der generalisierten Koordinate Φ, δΦ, ausdrücken:

δx₁ = a₁δΦ und δx₂ = a₂δΦ

Damit wird die virtuelle Arbeit:

(F₁a₁ - F₂a₂) δΦ = 0

Wegen der Willkürlichkeit von δΦ kann die linke Seite dieser Gleichung nur dann verschwinden, wenn der Klammerausdruck verschwindet, woraus letztlich folgt:

F₁a₁ = F₂a₂

Prinzip der virtuellen Arbeit für dynamische Systeme

Das Prinzip der virtuellen Arbeit kann auf bewegte Systeme erweitert werden, wenn man zu den eingeprägten Kräften die negativen Massenbeschleunigungen hinzunimmt (d'Alembertsches Prinzip). Dieses erweiterte Prinzip besagt, dass sich ein dynamisches System genau dann im dynamischen Gleichgewicht befindet, falls die virtuelle Arbeit δW für beliebige virtuelle Verschiebungen verschwindet. Aus der Bedingung δW ≡ 0 lassen sich Impuls- und Drallsatz herleiten, weshalb das Prinzip der virtuellen Arbeit als fundamentales Axiom der klassischen Mechanik betrachtet werden kann.

Aus dem dynamischen Problem $\dot{\mathbf{p}}_{i}=\mathbf{F}_{i}$

$0=\mathbf{F}_{i}-\dot{\mathbf{p}}_{i}=\mathbf{F}_{i}^{e}+\mathbf{F}_{i}^{z}-\dot{\mathbf{p}}_{i}$

wird ein statisches

$0=\left(\mathbf{F}_{i}-\dot{\mathbf{p}}_{i}\right)\cdot\delta\mathbf{x}_{i}=\left(\mathbf{F}_{i}^{e}+\mathbf{F}_{i}^{z}-\dot{\mathbf{p}}_{i}\right)\cdot\delta\mathbf{x}_{i}$

Bei einem statischen System kann man das Prinzip der virtuellen Arbeit anwenden

$\sum_{i=1}^{N}\mathbf{F}_{i}^{z}\cdot\delta\mathbf{x}_{i}=0$

und erhält somit das d'Alembertsches Prinzip:

$\sum_{i=1}^{N}\left(\mathbf{F}_{i}^{e}-\dot{\mathbf{p}}_{i}\right)\cdot\delta\mathbf{x}_{i}=0$

Literatur

• H. Goldstein: Klassische Mechanik. Wiley-VCH. ISBN 978-3527405893