Volterra-Gesetze

Die Lotka-Volterra-Regeln, auch Lotka-Volterra-Gesetze oder nur Volterra-Regeln genannt, umfassen drei Regeln zur quantitativen Beschreibung der Populationsdynamik in Räuber-Beute-Beziehungen.

Die den drei Regeln zugrundeliegenden mathematischen Lotka-Volterra-Gleichungen wurden 1925 und 1926 unabhängig voneinander von dem österreichisch-amerikanischen Mathematiker Alfred James Lotka und dem italienischen Mathematiker und Physiker Vito Volterra formuliert. Die drei Regeln finden sich als „Gesetze“ (loi) in Volterras 1931 veröffentlichten Buch; Volterra formuliert die Aussagen mathematisch präzise, und gibt eine strenge Herleitung aus den Gleichungen. In der biologischen Lehrbuchliteratur (siehe z. B. Müller 1991) finden sich unter der (in diesem Fall fälschlichen) Bezeichnung Lotka-Volterra-Regeln gelegentlich abweichende Aussagen, die aus den Gleichungen nicht begründbar sind.

Durch die Lotka-Volterra-Regeln wird die zahlenmäßige Entwicklung zweier Populationen unter interspezifischer Konkurrenz über große Zeiträume beschrieben. Alle drei Regeln gelten nur unter der Voraussetzung, dass lediglich zwischen den betrachteten beiden Arten eine Räuber-Beute-Beziehung besteht und die sonstigen biotischen und abiotischen Umweltfaktoren konstant oder zu vernachlässigen sind.

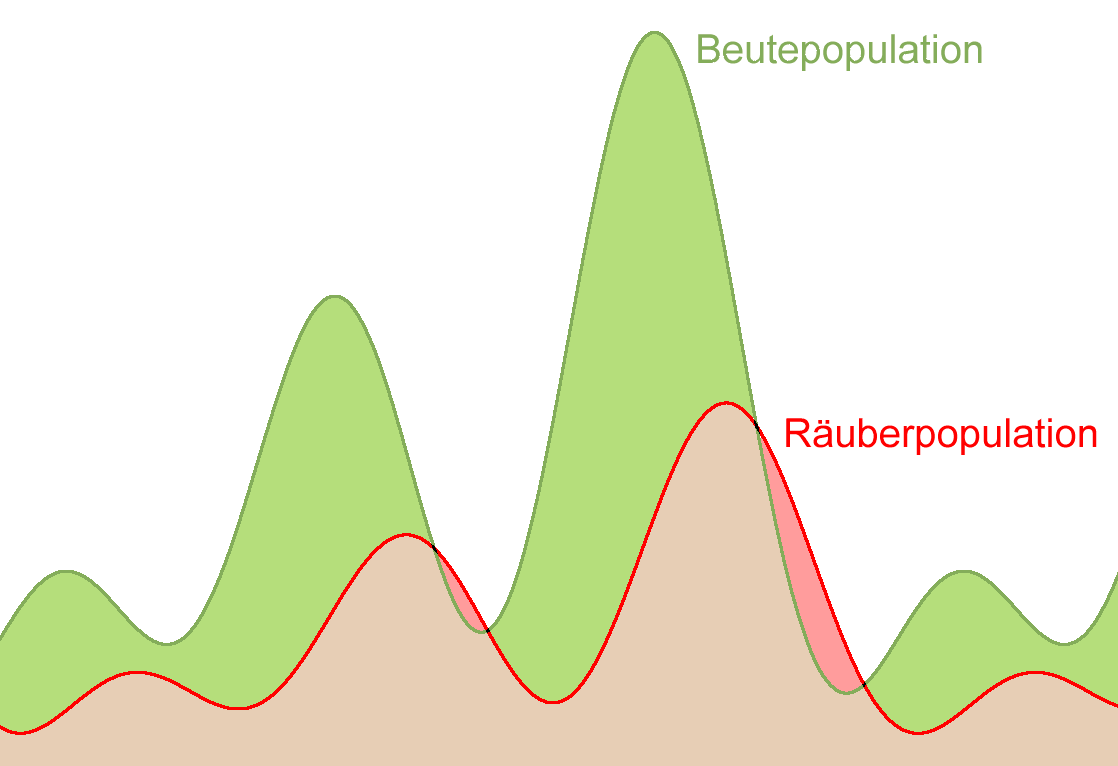
• Erste Lotka-Volterra-Regel (Periodische Populationsschwankung): Die Populationsgrößen von Räuber und Beute schwanken periodisch. Dabei folgen die Schwankungen der Räuberpopulation phasenverzögert denen der Beutepopulation. Die Länge der Perioden hängt von den Anfangsbedingungen und von den Wachstumsraten der Populationen ab.
• Zweite Lotka-Volterra-Regel (Konstanz der Mittelwerte): Die über genügend lange Zeiträume gemittelten Größen (Mittelwert) der Räuber- bzw. Beutepopulation sind konstant. Die Größe der Mittelwerte hängt nur von den Wachstums- und Schrumpfungsraten der Populationen, nicht aber von den Anfangsbedingungen ab.
• Dritte Lotka-Volterra-Regel (Störung der Mittelwerte): Werden Räuber- und Beutepopulation gleichermaßen proportional zu ihrer Größe dezimiert, so vergrößert sich kurzfristig der Mittelwert der Beutepopulation, während der Mittelwert der Räuberpopulation kurzfristig sinkt.

Die Lotka-Volterra-Regeln sind strenggenommen nur unter Beachtung ihrer selten erfüllten Voraussetzungen anwendbar. Trotzdem sind sie in der praktischen Ökologie von großer Bedeutung, weil sich zeigt, dass sie auch bei komplexeren Nahrungsbeziehungen und schwankenden Umweltfaktoren durchaus noch brauchbare Abschätzungen liefern.

Erste Lotka-Volterra-Regel

Die Erste Volterra-Regel besagt, dass die Individuenzahlen von Räuber und Beute bei ansonsten konstanten Bedingungen periodisch und zeitlich versetzt schwanken.

Populationsschwankungen bei Räuber und Beute

Die Populationskurven bilden also Wellen mit zeitlich versetzten Extrema, wobei die Kurve der Räuberpopulation nachlaufend ist. Z. B. folgt auf ein Maximum der Beutepopulation ein Maximum der Räuberpopulation. Grund dafür ist, dass bei einer hohen Anzahl von Beutetieren oder -pflanzen die Räuber mehr Nahrung und damit erhöhte Vermehrungschancen haben. Da die Jungtiere der Räuber einige Zeit zum Heranwachsen benötigen, kommt das Maximum der Räuber erst deutlich später zustande. Mit steigender Anzahl der Räuber wächst der Druck auf die Beutepopulation, sie schrumpft. Mit abnehmender Populationsdichte der Beute sinkt aber auch der Jagderfolg der Räuber, so dass auch deren Population mangels Nahrung absinkt. Der verringerte Feinddruck lässt nun wieder die Beutepopulation ansteigen usw.

Als Lehrbuchbeispiel für die Erste Volterra-Regel gelten die Fangaufzeichnungen der Hudson’s Bay Company, die über 90 Jahre lang geführt wurden. Danach schwankten der Eingang von Fellen von Luchsen (Räuber) und Schneeschuhhasen (Beute) mit einer Periode von 9,6 Jahren. Allerdings wird dieses Beispiel strenggenommen durch einen zweiten Räuber beeinflusst, nämlich die Jäger der Hudson’s Bay Company.

Mathematisch formuliert ergeben sich folgende gekoppelte Differentialgleichungen, die auch als Lotka-Volterra-Gleichungen bekannt sind:

a) Zeitliche Veränderung der Räuberpopulation

${dx \over dt} = Z_x \cdot x \cdot y - A_x \cdot x$

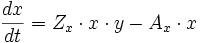
mit
x: Zahl der Räuber
y: Zahl der Beutetiere
x · y: Kontakthäufigkeit der beiden Arten
Z_x: Geburtenrate der Räuber
Z_x · x · y: Zuwachs der Räuber
A_x: Sterberate der Räuber
A_x · x: Abnahme der Räuber

b) Zeitliche Veränderung der Beutepopulation

${dy \over dt} = Z_y \cdot y - A_y \cdot x \cdot y$

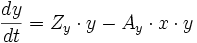
mit
Z_y: Geburtenrate der Beute
Z_y · y: Zuwachs der Beute
A_y: Sterberate der Beute
A_y · x · y: Abnahme der Beute

Man sieht bereits ohne Lösung der Differentialgleichungen, dass sich beide gegenseitig beeinflussen (Parameter x und y). So hängt der Zuwachs der Räuber sowohl von der generellen Geburtenrate als auch von der Wahrscheinlichkeit ab, mit der Räuber ein Beutetier fressen. Die Abnahme der Beute hängt nicht nur von der generellen Sterberate, sondern wiederum auch von der Kontakthäufigkeit ab.

Zweite Lotka-Volterra-Regel

Die Zweite Lotka-Volterra-Regel besagt, dass die durchschnittliche Größe der Populationen von Räuber und Beute in einer Räuber-Beute-Beziehung über einen längeren Zeitraum hinweg konstant ist, wenn die Umweltbedingungen ansonsten stabil sind.

Es ergibt sich mathematisch aus den grundlegenden Differentialgleichungen (siehe Erste Volterra-Regel).

Empirisch wurde auch die 2. Regel durch die Statistik der Hudson’s Bay Company zwischen 1845 und 1935 durch die Anzahl der eingelieferten Felle von Luchsen und Schneeschuhhasen belegt. Zwar schwankten die Zahlen der jährlich abgelieferten Felle bei Luchsen zwischen 1.000 und 70.000 sowie bei den Schneeschuhhasen zwischen 2.000 und 160.000, die Mittelwerte bei Betrachtung mehrerer Perioden liegen jedoch bei ca. 20.000 (Luchse) und 80.000 (Schneeschuhhasen).

Grundsätzlich gilt die Zweite Volterra-Regel unabhängig von den Anfangsgrößen der Population. Es ist auch im Experiment (z. B. mit verschiedenen Einzellern) reproduzierbar. Allerdings müssen in realen Systemen die Anfangsgrößen und das zur Verfügung stehende Gebiet mindestens so groß sein, dass sich (z. B. durch Verstecke) genügend Beutetiere auch bei hohem Fraßdruck halten, um die Reproduktionsfähigkeit zu sichern.

Dritte Lotka-Volterra-Regel

Die Dritte Lotka-Volterra-Regel trifft eine Aussage über die Auswirkungen einer Störung in einer Räuber-Beute-Beziehung. Werden Räuber- und Beutepopulation gleichzeitig dezimiert, so steigt der Mittelwert der Beutepopulation kurzfristig an, und der Mittelwert der Räuberpopulation sinkt kurzfristig ab.

Anders als bei periodischen Schwankungen fällt die Verminderung der Räuberpopulation zeitlich mit der Dezimierung der Beutepopulation zusammen. Nicht selten führt der Nahrungsmangel in dieser Situation zu einem Zusammenbruch der Räuberpopulation. Ohne Fressfeind findet die verbleibende Beutepopulation anschließend optimale Bedingungen und wächst schneller als sonst. Bis sich anschließend auch die Räuberpopulation wieder erholt, dauert es dagegen wegen der geringen Individuenzahl länger als üblich. In den meisten Räuber-Beute-Beziehungen kommt verstärkend hinzu, dass die Generationszeit von Räubern aufgrund ihrer Körpergröße länger ist als die ihrer Beutetiere.

Dieser Zusammenhang muss insbesondere bei Maßnahmen der Schädlingsbekämpfung beachtet werden. So bewirken beispielsweise Insektizide, dass nicht nur die Schädlinge sondern noch viel stärker deren Fressfeinde dezimiert werden. Im Endergebnis kann dies dazu führen, dass nach einer solchen Maßnahme der Schaden größer ist als ohne Bekämpfungsmaßnahmen.

Synthetische Gifte wie DDT, die zudem in Wirbeltieren akkumuliert werden, wirken sich wegen der langanhaltenden Wirkung besonders fatal aus.

Problematisch sind aber auch andere Insektizide, deren Giftwirkung z. B. in der Störung der Häutung der Insekten besteht. So können sowohl Juvenil-Hormone als auch Ecdysteroid-Hormone, die vielfach als scheinbar ökologisch verträglichere Mittel vorgeschlagen wurden, z. B. Laufkäfer, Raubwanzen und andere Raubinsekten zusätzlich zum Nahrungsmangel in ihrer Entwicklung ebenso schädigen wie ihre pflanzenfressenden Beutetiere. Aufgrund der Dritten Volterra-Regel führen sie zu einer langfristigen Schädigung des biologischen Gleichgewichts und die natürliche Schädlingskontrolle durch Fressfeinde wird verhindert.

Weiterführende Aussagen

Wie Volterra in seinem Buch bemerkt, folgen aus den mathematischen Formulierungen der Lotka-Volterra-Gleichung sogar noch weiterführende Aussagen:

• Wird nur die Räuberpopulation dezimiert, so erhöht sich kurzfristig der Mittelwert der Beutepopulation. Das langjährige Mittel der Räuber- und der Beutepopulation bleibt trotz der Dezimierung unverändert.
• Wird nur die Beutepopulation dezimiert (und bleibt die Dezimierungsrate unterhalb der Reproduktionsrate), so vermindert sich kurzfristig der Mittelwert der Räuberpopulation. Der langjährige Mittelwert der Räuber- und der Beutepopulation bleibt trotz der Dezimierung unverändert.

Literatur

• Vito Volterra: Leçons sur la Théorie Mathématique de la Lutte pour la Vie, Éditions Jaques Gabay 1990, ISBN 2-87647-066-7, autorisierter Nachdruck der bei Gauthier-Villars 1931 erschienen Originalausgabe. Die drei Gesetze werden auf den Seiten 15–27 behandelt.
• H.J. Müller: Ökologie, Gustav Fischer Verlag Jena, 2. Auflage 1991, Seite 224.