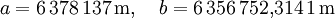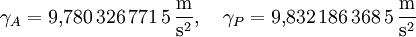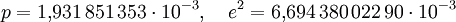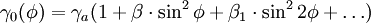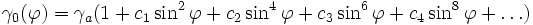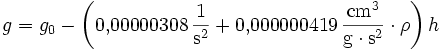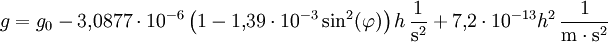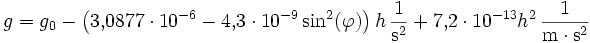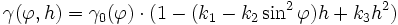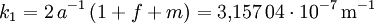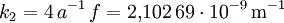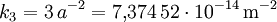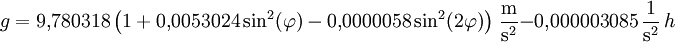- WELMEC–Formel
-
Normalschwereformeln sind mathematische Ausdrücke, mit denen die Schwerebeschleunigung an einem Punkt auf der Erde abgeschätzt werden kann.
Inhaltsverzeichnis
Normalschwere
Die Erdschwerebeschleunigung hängt von der Gravitationswirkung der Masse, die sich unterhalb des Gegenstandes befindet und der Zentrifugalbeschleunigung, die durch die Erdrotation hervorgerufen wird und der Anziehung entgegenwirkt, ab. Die Gravitationskraft nimmt mit Abstand zum Massenzentrum ab. Die Zentrifugalkraft nimmt mit Abstand von der Rotationsachse zu. Sie ist daher am Äquator am größten und nimmt zu den Polen hin ab. Die Formeln zur Berechnung der Normalschwere basieren auf der Annahme eines rotationssymetrisch aufgebauten Erdellipsoides, dessen Oberfläche gleichzeitig eine Äquipotentialfläche ist (Normalellipsoid), und sind daher nur von der Höhe und von der geographischen Breite abhängig.
Formel von Somigliana
Für die Normalschwere γ0 auf dem Niveauellipsoid gilt die Formel von Somigliana (1929) (nach Carlo Somigliana (1860-1955))
mit:
- γa = Normalschwere am Äquator
- γb = Normalschwere am Pol
- a = große Halbachse (Äquatorradius)
- b = kleine Halbachse (Polradius)
 = geographische Breite
= geographische Breite
Diese Formel lässt sich für numerische Zwecke umformen zu:
mit:
Für das Geodätische Referenzsystem 1980 (GRS 80) lauten die Parameter:
Näherungsformeln aus Reihenentwicklungen
Die Formel von Somigliana wurde durch verschiedene Reihenentwicklungen angenähert. Diese folgen dem Schema:
Internationale Schwereformel 1930
Die Normalschwereformel von Gino Cassinis wurde 1930 von der Internationalen Union für Geodäsie und Geophysik als Internationale Schwereformel zum Ellipsoid von Hayford bestimmt. Als Parameter galten:
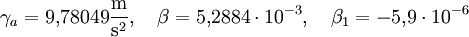 ;
;
Die Werte wurden im Laufe der Zeit durch neuere Erkenntnisse und genauere Messmethoden immer weiter verbessert.
Jeffreys verbesserte die Werte 1948 auf:
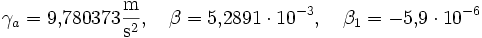 ;
;
Internationale Schwereformel 1967
Das Normalschwerefeld des Geodätischen Referenzsystem von 1967 ist definiert durch die Werte:
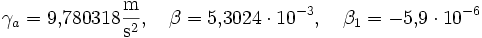 ;
;
Internationale Schwereformel 1980
Aus den Parametern des GRS 80 ergeben sich für die klassische Reihenentwicklung:
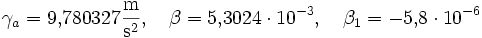 ;
;
Die Genauigkeit beträgt etwa ±10-6 m/s2.
Mit dem GRS 80 wurde auch folgende Reihenentwicklung eingeführt:
Die Parameter hierfür lauten:
- c1 = 5,279 0414·10−3
- c2 = 2,327 18·10−5
- c3 = 1,262·10−7
- c4 = 7·10−10
Diese Näherung ist auf etwa ±10-9 m/s2 genau. Wenn diese Genauigkeit nicht benötigt wird, können die hinteren Terme einfach weggelassen werden. Es ist jedoch zu empfehlen, die geschlossene Formel nach Somigliana zu verwenden.
Höhenabhängigkeit
Cassinis bestimmte die Höhenabhängigkeit zu:
Die mittlere Gesteinsdichte ρ wird heute bei der Normalschwere nicht mehr berücksichtigt.
Seit dem GRS 1967 gilt für die Höhenabhängigkeit von der Ellipsoidischen Höhe h:
bzw. ausmultipliziert:
Eine andere Darstellung lautet:
mit den Parametern aus GSR80 abgeleitet:
Diese Korrektur ist für fliegerische Höhen recht genau; für den Weltraum (über ca. 100 Kilometer) divergiert sie jedoch.
WELMEC-Formel
In allen deutschen Eichämtern wird heute der Bezugswert für die Fallbeschleunigung g in Bezug auf die mittlere geographische Breite φ und die mittlere Höhe über dem Meeresspiegel h nach der WELMEC–Formel berechnet:
Diese Formel basiert auf der Internationalen Schwereformel von 1967.
Beispiel
Fallbeschleunigung in Schweinfurt:
Daten:
- Geographische Breite: 50° 3′ 24″ = 50,0567°
- Höhe über Normalnull: 229,7 m
- Dichte der Gesteinsplatte: ca. 2,6 g/cm³
- Gemessene Fallbeschleunigung: g = 9,8100 ± 0,0001 m/s²
Errechnete Fallbeschleunigungen durch Normalschwereformeln:
- Cassinis: g = 9,81038 m/s²
- Jeffreys: g = 9,81027 m/s²
- WELMEC: g = 9,81004 m/s²
Literatur
- Wolfgang Torge: Geodäsie. Walter de Gruyter, Berlin u.a. 1975 ISBN 3-11-004394-7
- Wolfgang Torge: Geodäsie. 2. Auflage. Walter de Gruyter, Berlin u.a. 2003. ISBN 3-11-017545-2
Weblinks
- Uni Bonn: Normalfigur, Normalfeld (PDF, 558 KB)
- Roman Schwartz, Andreas Lindau: Das europäische Gravitationszonenkonzept nach WELMEC (PDF, 700 KB)
- H. Moritz: Geodetic Reference System 1980 (GRS80)
Wikimedia Foundation.

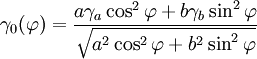
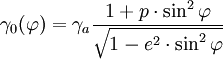
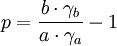
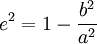 =
=