Bayes'sche Wahrscheinlichkeitstheorie

Der nach dem englischen Mathematiker Thomas Bayes benannte bayessche Wahrscheinlichkeitsbegriff (engl. Bayesianism) interpretiert Wahrscheinlichkeit als Grad persönlicher Überzeugung (engl. "degree of belief"). Er unterscheidet sich damit von den objektivistischen Wahrscheinlichkeitsauffassungen wie dem frequentistischen Wahrscheinlichkeitsbegriff, der Wahrscheinlichkeit als relative Häufigkeit interpretiert.

Der bayessche Wahrscheinlichkeitsbegriff darf nicht mit dem gleichfalls auf Thomas Bayes zurückgehenden Bayestheorem verwechselt werden, welches in der Statistik reiche Anwendung findet.

Entwicklung des bayesschen Wahrscheinlichkeitsbegriffs

Der bayessche Wahrscheinlichkeitsbegriff wird häufig verwendet, um die Plausibilität einer Aussage im Lichte neuer Erkenntnisse neu zu bemessen. Laplace (1812) entdeckte diesen Satz später unabhängig von Bayes und verwendete ihn, um Probleme in der Himmelsmechanik, in der medizinischen Statistik und, einigen Berichten zufolge, sogar in der Rechtsprechung zu lösen.

Zum Beispiel schätzte Laplace die Masse des Saturns auf Basis vorhandener astronomischer Beobachtungen seiner Umlaufbahn. Er erläuterte die Ergebnisse zusammen mit einem Hinweis seiner Unsicherheit: „Ich wette 11.000 zu 1, dass der Fehler in diesem Ergebnis nicht größer ist als 1/100 seines Wertes.“ (Laplace hätte die Wette gewonnen, denn 150 Jahre später musste sein Ergebnis auf Grundlage neuer Daten um lediglich 0,63 % korrigiert werden.)

Die bayessche Interpretation von Wahrscheinlichkeit wurde vor allem in England früh ausgearbeitet. Führende Köpfe waren etwa Harold Jeffreys und Frank Plumpton Ramsey. Letzterer entwickelte einen Ansatz, den er aufgrund seines frühen Todes nicht weiter verfolgen konnte, der aber unabhängig davon von Bruno de Finetti in Italien aufgenommen wurde. Grundgedanke ist, „vernünftige Einschätzungen“ (engl. rational belief) als eine Verallgemeinerung von Wettstrategien aufzufassen: Gegeben sei eine Menge von Information/Messungen/Datenpunkten, und gesucht wird eine Antwort auf die Frage, wie hoch man auf die Korrektheit seiner Einschätzung wetten oder welche Odds man geben würde. (Der Hintergrund ist, dass man gerade dann viel Geld wettet, wenn man sich seiner Einschätzung sicher ist. Diese Idee hatte großen Einfluss auf die Spieltheorie). Eine Reihe von Streitschriften gegen (frequentistische) statistische Methoden ging von diesem Grundgedanken aus, über den seit den 1950ern zwischen Bayesianern und Frequentisten debattiert wird.

Formalisierung des Wahrscheinlichkeitsbegriffes

Ist man bereit, Wahrscheinlichkeit als "Sicherheit in der persönlichen Einschätzung eines Sachverhaltes" zu interpretieren (s.o.), so stellt sich die Frage, welche logischen Eigenschaften diese Wahrscheinlichkeit haben muss, um nicht widersprüchlich zu sein. Wesentliche Beiträge wurden hierzu von Cox (1946) geleistet. Er fordert die Gültigkeit der folgenden Prinzipien:

1. Transitivität: Wenn Wahrscheinlichkeit A größer ist als Wahrscheinlichkeit B, und Wahrscheinlichkeit B größer als Wahrscheinlichkeit C, dann muss Wahrscheinlichkeit A auch größer als Wahrscheinlichkeit C sein. Ohne diese Eigenschaft wäre es nicht möglich, Wahrscheinlichkeiten in reellen Zahlen auszudrücken, denn reelle Zahlen sind eben transitiv angeordnet. Außerdem würden Paradoxien wie die folgende auftreten: Ein Mann, der die Transitivität der Wahrscheinlichkeit nicht versteht, hat in einem Rennen auf Pferd A gesetzt. Er glaubt jetzt aber, Pferd B sei besser, und tauscht seine Karte um. Er muss etwas dazuzahlen, aber das macht ihm nichts aus, weil er jetzt eine bessere Karte hat. Dann glaubt er, Pferd C sei besser als Pferd B. Wieder tauscht er um und muss etwas dazuzahlen. Jetzt glaubt er aber, Pferd A sei besser als Pferd C. Wieder tauscht er um und muss etwas dazuzahlen. Immer glaubt er, er bekäme eine bessere Karte, aber jetzt ist alles wieder wie vorher, nur ist er ärmer geworden.
2. Negation: Wenn wir über die Wahrheit von etwas eine Erwartung haben, dann haben wir implizit auch eine Erwartung über dessen Unwahrheit.
3. Konditionierung: Wenn wir eine Erwartung haben über die Wahrheit von H, und auch eine Erwartung über die Wahrheit von D im Falle, dass H wahr wäre, dann haben wir implizit auch eine Erwartung über die gleichzeitige Wahrheit von H und D.
4. Schlüssigkeit (soundness): Wenn es mehrere Methoden gibt, bestimmte Informationen zu benutzen, dann muss die Schlussfolgerung immer dieselbe sein.

Wahrscheinlichkeitswerte

Es stellt sich heraus, dass die folgenden Regeln für Wahrscheinlichkeitswerte W(H) gelten müssen:

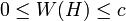1. $0 \le W(H) \le c$ Wir wählen c = 1.
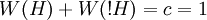2. $\!\,W(H) + W(!H) = c = 1$ 'Summenregel'
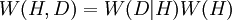3. $\!\,W(H,D) = W(D| H) W(H)$ 'Produktregel'

Hier bedeutet:

• H oder D: Die Hypothese H ist wahr (oder das Ereignis H tritt ein) oder das Ereignis D ist eingetreten.
• W(H): Die Wahrscheinlichkeit, dass Hypothese H wahr ist oder Ereignis H eintreten wird.
• !H: Nicht H: die Hypothese H ist nicht wahr oder das Ereignis H tritt nicht ein.
• H,D: H und D sind beide wahr oder treten beide ein oder eins ist wahr und der andere tritt ein.
• W(D | H): Die Wahrscheinlichkeit, dass Hypothese D wahr ist oder Ereignis D eintreten wird im Fall, dass H wahr wäre oder eintreten würde.

Man kann leicht einsehen, dass die Wahrscheinlichkeitswerte bei 0 anfangen müssen; sonst würde so etwas wie eine 'doppelt so große Wahrscheinlichkeit' keine Bedeutung haben.

Beispiel: Bei einem Wurf mit einem Würfel mit 6 gleichen Flächen ist die Wahrscheinlichkeit, eine 1 oder eine 3 zu werfen, doppelt so groß wie die Wahrscheinlichkeit, eine 4 zu werfen, weil es sich dabei eben um zwei Flächen handelt im Vergleich zu nur einer solchen Fläche.

Aus den obigen Regeln der Wahrscheinlichkeitswerte lassen sich andere ableiten.

Praktische Bedeutung in der Statistik

Im Gegensatz zum frequentistischen Wahrscheinlichkeitsbegriff lässt die bayessche Interpretation zu, dass man den Wert unzufälliger Konstanten schätzt, wie zum Beispiel die Masse des Saturns. In der frequentistischen Interpretation ist das streng genommen nicht möglich (s.o.), weil dort Wahrscheinlichkeiten mittels Häufigkeiten interpretiert werden.

Um solche Probleme trotzdem im Rahmen der frequentistischen Interpretation angehen zu können, wird die Unsicherheit dort mittels einer eigens dazu erfundenen variablen Zufallsgröße beschrieben. Die Bayes'sche Wahrscheinlichkeitstheorie benötigt solch eine Hilfsgröße nicht. Stattdessen führt sie das Konzept der A-priori-Wahrscheinlichkeit ein, die Vorwissen und Grundannahmen des Beobachters in einer Wahrscheinlichkeitsverteilung zusammenfasst. Vertreter des Bayes-Ansatzes sehen es als großen Vorteil, dass Vorwissen und A-Priori-Annahmen explizit im Modell ausgedrückt werden.

Weblinks und Referenzen

• David MacKay: Information Theory, Inference, and Learning Algorithms, ISBN 0-521-64298-1, insb. Kapitel 37: Bayesian Inference and Sampling Theory
• Jonathan Weisberg: Varieties of Bayesianism, In: Dov Gabbay, Stephan Hartmann, John Woods (Hgg): Handbook of the History of Logic, Bd. 10, vorauss. 2008
• http://www.ap.univie.ac.at/users/fe/Lehre/aussermathAnw/Bayes.html
• David Howie: Interpreting Probability, Controversies and Developments in the Early Twentieth Century, Cambridge University Press, 2002, ISBN 0-521-81251-8
• D.S. Sivia: Data Analysis: A Bayesian Tutorial, Oxford Science Publications, 2006, ISBN 0-19-856831-2, besonders für Probleme aus der Physik zu empfehlen.