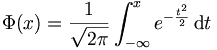Wahrscheinlichkeitspapier
- Wahrscheinlichkeitspapier
-
Das Wahrscheinlichkeitsnetz oder Wahrscheinlichkeitspapier gehört zu den mathematischen Papieren. Mit einem Wahrscheinlichkeitspapier kann man die Daten eines statistischen Merkmals daraufhin untersuchen, ob ihnen eine bestimmte Wahrscheinlichkeitsverteilung zu Grunde liegt. Es ist mit einem Koordinatennetz versehen, in dem auf der Abszisse die Quantile der Verteilung äquidistant, dagegen auf der Ordinate die dazugehörigen Funktionswerte der Verteilung in linearisierter Form abgetragen sind. Beim Eintragen der Wertepaare (Quantil, Verteilung) erhält man so eine Gerade.
Das Wahrscheinlichkeitsnetz ist ein herkömmliches Hilfsmittel, das vor allem vor Einführung der elektronischen Datenverarbeitung breite Anwendung fand, um einigermaßen schnell und effizient eine Verteilungsüberprüfung von Daten zur erreichen. Allgemein bekannt ist vor allem das Wahrscheinlichkeitsnetz der Normalverteilung, aber auch die Weibullverteilung wird in Wahrscheinlichkeitsnetzen dargestellt.
Die Normalverteilung im Wahrscheinlichkeitsnetz
Auf der Abszisse werden die Quantile x einer standardnormalverteilten Zufallsvariablen abgetragen, ebenso auf der Ordinate. Auf der Ordinate werden aber nicht die Werte von x, sondern deren Verteilungsfunktionswerte
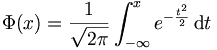
angezeigt. Ordnet man auf der Ordinate die Skalenstriche so an, dass rechnerisch die Abstände zwischen den Verteilungsfunktionswerten gleich groß sind, erhält man das typische Muster des Gaußschen Wahrscheinlichkeitsnetzes.
Durch diese Linearisierung ergibt sich für die Wertepaare (x;Φ(x)) eine Gerade. Wahrscheinlichkeitspapier ermöglicht also ein einfaches Zeichnen einer solchen Funktion, beziehungsweise die einfache Prüfung, ob gegebene Wertepaare zu einer Normalverteilung passen (sie müssen dann auf einer Geraden liegen).
Als Beispiel ist nachfolgend die Funktion für den Mittelwert μ = 100 und die Streuung σ = 20 auf Wahrscheinlichkeitspapier gezeichnet.
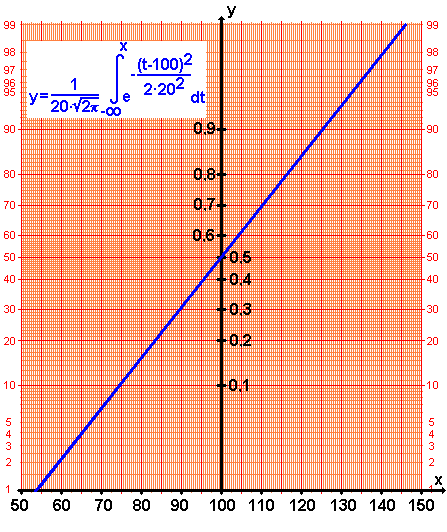
Praktische Anwendung am Beispiel der Normalverteilung
Praktisch wird so vorgegangen, dass die n erhobenen Beobachtungswerte xi der Größe nach geordnet werden. Den geordneten Werten (x[i]) werden dann die dazugehörigen Werte der relativen Summenfunktion 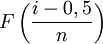 zugeordnet. Ergibt sich aus den Wertepaaren annähernd eine Gerade, kann für die Daten eine zu Grunde liegende Normalverteilung vermutet werden.
zugeordnet. Ergibt sich aus den Wertepaaren annähernd eine Gerade, kann für die Daten eine zu Grunde liegende Normalverteilung vermutet werden.
Literatur
- Hartung, Joachim, Elpelt, Bärbel, Klösener, Karl-Heinz: Statistik, München 2002
- J. M. Chambers, W. S. Cleveland, Beat Kleiner, Paul A. Tukey: Graphical Methods for Data Analysis, Wadsworth, 1983.
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Wahrscheinlichkeitsplot — Das Wahrscheinlichkeitsnetz oder Wahrscheinlichkeitspapier gehört zu den mathematischen Papieren. Mit einem Wahrscheinlichkeitspapier kann man die Daten eines statistischen Merkmals daraufhin untersuchen, ob ihnen eine bestimmte… … Deutsch Wikipedia
Wahrscheinlichkeitsnetz — Das Wahrscheinlichkeitsnetz oder Wahrscheinlichkeitspapier gehört zu den mathematischen Papieren. Mit einem Wahrscheinlichkeitspapier kann man die Daten eines statistischen Merkmals daraufhin untersuchen, ob ihnen eine bestimmte… … Deutsch Wikipedia
Log-Normalverteilung — Die logarithmische Normalverteilung (kurz Log Normalverteilung) ist eine kontinuierliche Wahrscheinlichkeitsverteilung über der Menge der positiven reellen Zahlen. Sie beschreibt die Verteilung einer Zufallsvariablen X, wenn ln(X) normalverteilt… … Deutsch Wikipedia
Log normalverteilung — Die logarithmische Normalverteilung (kurz Log Normalverteilung) ist eine kontinuierliche Wahrscheinlichkeitsverteilung über der Menge der positiven reellen Zahlen. Sie beschreibt die Verteilung einer Zufallsvariablen X, wenn ln(X) normalverteilt… … Deutsch Wikipedia
Logarithmuspapier — Logarithmenpapier gehört zu den mathematischen Papieren (auch: Netzpapier) und ist mit einem Koordinatennetz überzogen, so dass auf ihm Koordinaten auf einfache Weise dargestellt werden können. Es kann entweder für beide Achsen die logarithmische … Deutsch Wikipedia
Lognormal-Verteilung — Die logarithmische Normalverteilung (kurz Log Normalverteilung) ist eine kontinuierliche Wahrscheinlichkeitsverteilung über der Menge der positiven reellen Zahlen. Sie beschreibt die Verteilung einer Zufallsvariablen X, wenn ln(X) normalverteilt… … Deutsch Wikipedia
Lognormale Verteilung — Die logarithmische Normalverteilung (kurz Log Normalverteilung) ist eine kontinuierliche Wahrscheinlichkeitsverteilung über der Menge der positiven reellen Zahlen. Sie beschreibt die Verteilung einer Zufallsvariablen X, wenn ln(X) normalverteilt… … Deutsch Wikipedia
Lognormalverteilung — Die logarithmische Normalverteilung (kurz Log Normalverteilung) ist eine kontinuierliche Wahrscheinlichkeitsverteilung über der Menge der positiven reellen Zahlen. Sie beschreibt die Verteilung einer Zufallsvariablen X, wenn ln(X) normalverteilt… … Deutsch Wikipedia
Logarithmenpapier — (auch logarithmisches Papier) gehört zu den mathematischen Papieren (auch: Netzpapier) und ist mit einem Koordinatennetz überzogen, so dass auf ihm Koordinaten auf einfache Weise dargestellt werden können. Es kann entweder für eine oder beide… … Deutsch Wikipedia
Logarithmische Darstellung — Verteilung der Beitragszahlen der aktivsten Autoren in der deutschsprachigen Wikipedia Die logarithmische Darstellung basiert auf einer Skale, die nicht den Wert einer physikalischen Größe verwendet, sondern den Logarithmus ihres Zahlenwerts. Bei … Deutsch Wikipedia
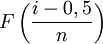 zugeordnet. Ergibt sich aus den Wertepaaren annähernd eine Gerade, kann für die Daten eine zu Grunde liegende Normalverteilung vermutet werden.
zugeordnet. Ergibt sich aus den Wertepaaren annähernd eine Gerade, kann für die Daten eine zu Grunde liegende Normalverteilung vermutet werden.