Wedge-Produkt (Topologie) — Mit dem Wedge Produkt (nach wedge engl. Keil; auch Einpunktvereinigung oder Bouquet genannt) zweier punktierter topologischer Räume X und Y bezeichnet man ihre disjunkte Vereinigung, die an einem Punkt (dem Basispunkt) verklebt ist. Formal ist… … Deutsch Wikipedia
Wedge — (von englisch wedge = „Keil“) bezeichnet: im Golfsport Schläger für kürzere Distanzen, siehe Golfschläger#Wedges in der Tontechnik keilförmige Lautsprecher für die Bühnen, siehe Monitoring (Tontechnik) in der Medizin den Druck beim Verschließen… … Deutsch Wikipedia
Smash-Produkt — Das Smash Produkt bezeichnet eine topologische Konstruktion. Für zwei gegebene punktierte topologische Räume X und Y mit Basispunkten x0 und y0 betrachtet man zunächst den Produktraum X × Y mit der Identifizierung (x, y0) ∼ (x0, y) für alle x ∈ X … Deutsch Wikipedia
Freies Produkt — In der Algebra versteht man unter dem freien Produkt eine bestimmte Konstruktion einer Gruppe aus zwei oder mehr gegebenen Gruppen. Man kann sich das freie Produkt als eine nicht kommutative Entsprechung der direkten Summe vorstellen, ungefähr… … Deutsch Wikipedia
Wedgeprodukt — Wedge (von englisch wedge = „Keil“) bezeichnet: im Golfsport Schläger für kürzere Distanzen, siehe Golfschläger#Wedges in der Bühnentechnik keilförmige Boxen, siehe Monitoring (Beschallung) in der Medizin den Druck beim Verschließen der… … Deutsch Wikipedia
Eilenberg-Steenrod-Axiome — Der Begriff der Homologietheorie stammt aus der algebraischen Topologie und charakterisiert axiomatisch die Weise, wie beispielsweise die Singuläre Homologie oder die Bordismustheorien topologischen Räumen abelsche Gruppen zuordnen… … Deutsch Wikipedia
Einpunktvereinigung — Mit dem Wedge Produkt (nach wedge engl. Keil; auch Einpunktvereinigung oder Bouquet genannt) zweier punktierter topologischer Räume X und Y bezeichnet man ihre disjunkte Vereinigung, die an einem Punkt (dem Basispunkt) verklebt ist. Formal ist… … Deutsch Wikipedia
Satz von Stokes — Der Satz von Stokes oder stokesscher Integralsatz ist ein nach Sir George Gabriel Stokes benannter Satz aus der Differentialgeometrie. In der allgemeinen Fassung handelt es sich um einen sehr tiefliegenden Satz über die Integration von… … Deutsch Wikipedia
Abbildungskegel — Der Abbildungskegel ist eine Konstruktion in der Topologie, die einer Abbildung zwischen zwei topologischen Räumen einen dritten topologischen Raum Cf zuordnet. Der Abbildungskegel Hierzu definiert man zunächst den … Deutsch Wikipedia
Punktierter Raum — Ein punktierter topologischer Raum ist ein Paar (X,x0), bestehend aus einem topologischen Raum X und einem Punkt x0 in X (Grundpunkt, Basispunkt, ausgezeichneter Punkt). Eine punktierte (stetige) Abbildung (X,x0) → (Y,y0) ist eine stetige… … Deutsch Wikipedia
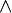 und
und 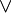
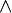 ) der Graßmann-Algebra (engl.: wedge product) in der Differentialgeometrie
) der Graßmann-Algebra (engl.: wedge product) in der Differentialgeometrie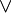 ) in der Kategorie der punktierten topologischen Räume (engl.: wedge sum)
) in der Kategorie der punktierten topologischen Räume (engl.: wedge sum)