- Abbildungskegel
-
Der Abbildungskegel ist eine Konstruktion in der Topologie, die einer Abbildung
 zwischen zwei topologischen Räumen einen dritten topologischen Raum Cf zuordnet.
zwischen zwei topologischen Räumen einen dritten topologischen Raum Cf zuordnet.Hierzu definiert man zunächst den Kegel CX eines Raumes X. Hierunter versteht man den Raum, den man aus dem Produkt
![X\times [0,1]](f/7ff959d5b1233da08ed4a5475eb52233.png) durch Identifikation aller Punkte in
durch Identifikation aller Punkte in  (der „Kegelspitze“) erhält. Dieser ist offenbar homotopieäquivalent zu einem Punkt.
(der „Kegelspitze“) erhält. Dieser ist offenbar homotopieäquivalent zu einem Punkt.Den Abbildungskegel einer Abbildung
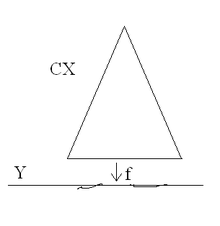
 erhält man nun (wie in der Zeichnung angedeutet) durch Verkleben von CX und Y. Genauer identifiziert man in der disjunkten Vereinigung
erhält man nun (wie in der Zeichnung angedeutet) durch Verkleben von CX und Y. Genauer identifiziert man in der disjunkten Vereinigung  jeweils (x,0) mit f(x) für alle
jeweils (x,0) mit f(x) für alle  .
.In der Kategorie der punktierten topologischen Räume betrachtet man meist den reduzierten Abbildungskegel. Dieser entsteht dadurch, dass man in dem Abbildungskegel Cf das Intervall
![pt \times [0,1]](2/3f254f4ccddccce1a7698c6b0d6ad679.png) identifiziert. Hierbei bezeichnet pt den Basispunkt von X. Für einen wohlpunktierten Raum ist der reduzierte Abbildungskegel homotopieäquivalent zum normalen Abbildungskegel.
identifiziert. Hierbei bezeichnet pt den Basispunkt von X. Für einen wohlpunktierten Raum ist der reduzierte Abbildungskegel homotopieäquivalent zum normalen Abbildungskegel.Beispiel
Wenn
 , so gilt
, so gilt  . Ist
. Ist  konstant, so gilt
konstant, so gilt  , wobei
, wobei  das Wedge-Produkt bezeichnet.
das Wedge-Produkt bezeichnet.Der Kegel CSn − 1 ist homöomorph zur Vollkugel Dn. Dies sieht man, indem man die Kegelspitze "herunterdrückt". Allgemeiner gilt, dass, wenn
 die anklebende Abbildung in einem CW-Komplex X an das n-Skelett ist, der Abbildungskegel Cf homöomorph zum (n+1)-Skelett Xn + 1 ist.
die anklebende Abbildung in einem CW-Komplex X an das n-Skelett ist, der Abbildungskegel Cf homöomorph zum (n+1)-Skelett Xn + 1 ist.Rolle in der Homotopietheorie
Sind zwei Abbildungen
 homotop, so sind ihre Abbildungskegel Cf und Cg homotopieäquivalent.
homotop, so sind ihre Abbildungskegel Cf und Cg homotopieäquivalent.Wenn
 ein abgeschlossener Teilraum und die Inklusion
ein abgeschlossener Teilraum und die Inklusion  eine Kofaserung ist, so ist Ci homotopieäquivalent zu dem Quotientenraum X / A. Man kann zeigen, dass die Inklusion
eine Kofaserung ist, so ist Ci homotopieäquivalent zu dem Quotientenraum X / A. Man kann zeigen, dass die Inklusion  stets eine abgeschlossene Kofaserung ist. Somit erhält man, dass der Abbildungskegel Cj homotopieäquivalent zu
stets eine abgeschlossene Kofaserung ist. Somit erhält man, dass der Abbildungskegel Cj homotopieäquivalent zu  ist, wobei ΣX die Einhängung von X bezeichnet. Fährt man auf die gleiche Weise fort, so erhält man, dass der Abbildungskegel der Inklusion von Cf nach ΣX die Einhängung von Y ergibt usw.
ist, wobei ΣX die Einhängung von X bezeichnet. Fährt man auf die gleiche Weise fort, so erhält man, dass der Abbildungskegel der Inklusion von Cf nach ΣX die Einhängung von Y ergibt usw.Hat man eine Abbildung
 in einen topologischen Raum Z, so ist die Komposition
in einen topologischen Raum Z, so ist die Komposition  genau dann homotop zu einer konstanten Abbildung, wenn g fortsetzbar ist zu einer Abbildung
genau dann homotop zu einer konstanten Abbildung, wenn g fortsetzbar ist zu einer Abbildung  . Für den Fall, dass
. Für den Fall, dass  ist das Resultat noch etwas anschaulicher: eine Abbildung
ist das Resultat noch etwas anschaulicher: eine Abbildung  ist genau dann homotop zu einer konstanten Abbildung, wenn sie fortsetzbar ist zu einer Abbildung
ist genau dann homotop zu einer konstanten Abbildung, wenn sie fortsetzbar ist zu einer Abbildung  . Um die Abbildung g' zu konstruieren, benutzt man einfach die Homotopie
. Um die Abbildung g' zu konstruieren, benutzt man einfach die Homotopie ![H: X\times [0,1]\rightarrow Z](0/5f0dd6dfbdbaafe0c7f7c6c3357e4c01.png) , die auf
, die auf  konstant ist.
konstant ist.Wenn man punktierte Räume und punktierte Abbildungen betrachtet, bedeutet dies, dass die folgende Sequenz exakt ist:
Diese exakte Sequenz nennt man auch Puppe-Folge.
Literatur
- Glen E. Bredon: Topology and Geometry. Revised 3rd printing. Springer, New York u. a. 1997, ISBN 0-387-97926-3 (Graduate Texts in Mathematics 139).
- Robert M. Switzer: Algebraic Topology – Homology and Homotopy. Reprint of the 1975 edition. Springer, Berlin u. a. 2002, ISBN 3-540-42750-3 (Classics in Mathematics).
-
Wikimedia Foundation.

![\dots \rightarrow [\Sigma Y, Z] \rightarrow [\Sigma X, Z] \rightarrow [Cf, Z] \rightarrow [Y, Z] \rightarrow [X, Z]](6/48640822e513f5cfcf3d165c9f18c9e1.png)