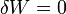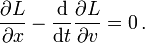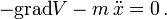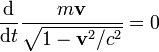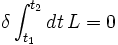- Wirkungsfunktional
-
Das Hamiltonsche Prinzip oder das Prinzip der kleinsten Wirkung ist ein Extremalprinzip. Danach verhalten sich die physikalischen Teilchen und Felder so, dass eine Größe, die die Teilchenbahnen und Felder bewertet, kleiner ist als bei allen anderen denkbaren Teilchenbahnen oder Feldwerten. Die Bewertung nennen Physiker die Wirkung, mathematisch ist die Wirkung ein Funktional. Genauer gesehen erweist sich in vielen Fällen die Wirkung nicht als minimal, sondern nur als stationär. Dann ist das Hamiltonsche Prinzip ein Prinzip der stationären Wirkung.
Ein Beispiel ist das Fermatsche Prinzip, nach dem ein Lichtstrahl in einem Medium von allen denkbaren Wegen vom Anfangspunkt zum Endpunkt den Weg mit der geringsten Laufzeit durchläuft.
Aus dem Hamiltonschen Prinzip folgen bei geeignet gewählter Wirkung die Newtonschen Bewegungsgleichungen, aber auch die Gleichungen der relativistischen Mechanik, die Maxwellgleichungen der Elektrodynamik, die Einstein-Gleichungen der Allgemeinen Relativitätstheorie und die Gleichungen, mit denen man die anderen elementaren Wechselwirkungen beschreibt.
Inhaltsverzeichnis
Geschichte
Pierre Maupertuis sprach 1746 als erster von einem allgemeingültigen Prinzip der Natur, extremal oder optimal abzulaufen (vgl. auch Ockhams Rasiermesser). Leonhard Euler und Joseph Lagrange klärten in der Mitte des achtzehnten Jahrhunderts, dass solch ein Prinzip die Gültigkeit von Euler-Lagrange-Gleichungen bedeute. Die lagrangesche Formulierung der Mechanik stammt von 1788. 1834 formulierte William Hamilton das nach ihm benannte Prinzip.
Mathematische Beschreibung
In der Mechanik ist die Wirkung das zeitliche Integral über eine Funktion der Zeit t, des Ortes
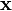 und der Geschwindigkeit
und der Geschwindigkeit 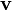 , die sogenannte Lagrangefunktion
, die sogenannte LagrangefunktionBeispielsweise ist in Newtonscher Mechanik die Lagrangefunktion eines Teilchens der Masse
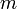 , das sich im Potential
, das sich im Potential 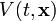 bewegt, die Differenz von kinetischer und potentieller Energie:
bewegt, die Differenz von kinetischer und potentieller Energie:In der relativistischen Mechanik ist die Lagrangefunktion eines freien Teilchens
Jeder Bahn
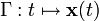 , die im Laufe der Zeit t von einem Anfangspunkt
, die im Laufe der Zeit t von einem Anfangspunkt 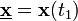 zu einem Endpunkt
zu einem Endpunkt 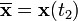 durchlaufen wird, ordnet die Wirkung folgenden Wert zu:
durchlaufen wird, ordnet die Wirkung folgenden Wert zu:Die Wirkung
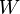 hat also die Dimension Energie mal Zeit.
hat also die Dimension Energie mal Zeit.Das Hamiltonsche Prinzip besagt nun, dass von allen denkbaren Bahnen, die anfänglich durch
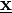 und schließlich durch
und schließlich durch 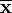 laufen, diejenigen Bahnen in der Natur durchlaufen werden, die die kleinste, genauer eine stationäre Wirkung haben. Für die physikalisch durchlaufenen Bahnen verschwindet die erste Variation der Wirkung:
laufen, diejenigen Bahnen in der Natur durchlaufen werden, die die kleinste, genauer eine stationäre Wirkung haben. Für die physikalisch durchlaufenen Bahnen verschwindet die erste Variation der Wirkung:Sie genügen daher der Euler-Lagrange-Gleichung
Beispielsweise ergeben sich für die nichtrelativistische Bewegung eines Teilchens im Potential die Newtonschen Bewegungsgleichungen
Bei einem freien, relativistischen Teilchen ist der Impuls dagegen zeitunabhängig:
Das Hamiltonsche Prinzip für Felder
In der Feldtheorie wird hingegen das Verhalten von Feldern untersucht, d.h. auf welche Weise sie sich verändern und mit ihrer Umgebung wechselwirken.
Setzt man in das Hamiltonsche Prinzip
die Lagrange-Dichte über
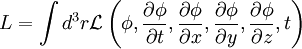 , mit einem Feld φ = φ(x,y,z,t)
, mit einem Feld φ = φ(x,y,z,t)
ein, so erhält man das Hamiltonsche Prinzip für Felder, mit
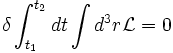 .
.
Man erkennt, dass diese Formulierung insbesondere für die Relativitätstheorie interessant ist, da hier über den Ort und die Zeit integriert wird. Analog zum gewöhnlichen Hamiltonschen Prinzip lassen sich aus dieser abgewandelten Version die Lagrangegleichungen für Felder bestimmen.
Eigenschaften
Da das Wirkungsprinzip unabhängig vom verwendeten Koordinatensystem ist, kann man die Euler-Lagrangegleichungen in solchen Koordinaten untersuchen, die dem jeweiligen Problem angemessen sind und beispielsweise Kugelkoordinaten verwenden, wenn es um die Bewegung im drehinvarianten Gravitationsfeld der Sonne geht. Dies vereinfacht die Lösung der Gleichung.
Zudem lassen sich bequem Zwangsbedingungen berücksichtigen, wenn mechanische Vorrichtungen die freie Bewegung der Massepunkte einschränken wie beispielsweise die Aufhängung bei einem Kugelpendel.
Vor allem aber lässt sich in dieser Formulierung der Bewegungsgleichungen das Noether-Theorem beweisen, das besagt, dass zu jeder Symmetrie der Wirkung eine Erhaltungsgröße gehört und dass umgekehrt zu jeder Erhaltungsgröße eine Symmetrie der Wirkung gehört.
Die Erhaltungsgrößen wiederum sind ausschlaggebend dafür, ob sich die Bewegungsgleichungen durch Integrale über gegebene Funktionen lösen lassen.
Weblinks
Wikimedia Foundation.

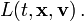
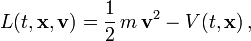
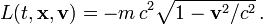
![W[\Gamma] =
\int_{t_1}^{t_2} \mathrm d t\,
\,L\bigl(t,\mathbf x(t),\mathbf \dot{x}(t)\bigr)\,.](/pictures/dewiki/101/e61c461fdf3d0068ade1f4ee4079c0cb.png)