Woodall-Zahl

Eine Cullen-Zahl ist eine Zahl der Form 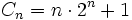$C_n = n \cdot 2^n + 1$. Mit diesen Zahlen hat sich Reverend James Cullen 1905 beschäftigt. Ihm fiel auf, dass außer C₁=3 alle Zahlen dieser Form bis C₉₉ zusammengesetzte Zahlen, also keine Primzahlen sind. Seine Unsicherheit bezüglich C₅₃ konnte von Allan J.C. Cunningham 1906 ausgeräumt werden, indem dieser den Teiler 5591 fand. Cunningham zeigte, dass alle C_n bis n=200 zusammengesetzt sind, mit einer möglichen Ausnahme für n=141.

1958 bestätigte Raphael M. Robinson, dass C₁₄₁ eine Primzahl ist und wies nach, dass mit Ausnahme von C₁ und C₁₄₁ alle Cullen-Zahlen von C₁ bis C₁₀₀₀ zusammengesetzte Zahlen sind.

Wilfrid Keller hat 1984 gezeigt, das C₄₇₁₃, C₅₇₉₅, C₆₆₁₁ und C₁₈₄₉₆ ebenfalls Primzahlen sind, aber alle anderen C_n mit n ≤ 30000 zusammengesetzte Cullen-Zahlen sind.

Inzwischen (Juli 2008) ist bekannt, dass C_n für folgende n Primzahlen sind: 32292, 32469, 59656, 90825, 262419, 361275, 481899 und 1354828. Außer diesen gibt es keine Cullen-Primzahlen bis n=3500000.

Es wird vermutet, dass es unendlich viele Cullen-Primzahlen gibt.

Woodall-Zahl

Eine Zahl der Form 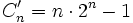$C'_n = n \cdot 2^n - 1$ wird Cullen-Zahl der zweiten Art oder auch Woodall-Zahl genannt (nach H.J. Woodall, der sie 1917 beschrieb).

Im Bereich von n <= 20000 sind nur die Woodall-Zahlen C^'₂, C^'₃, C^'₆, C^'₃₀, C^'₇₅, C^'₈₁, C^'₁₁₅, C^'₁₂₃, C^'₂₄₉, C^'₃₆₂, C^'₃₈₄, C^'₄₆₂, C^'₅₁₂, C^'₇₅₁, C^'₈₈₂, C^'₅₃₁₂, C^'₇₇₅₅, C^'₉₅₃₁, C^'₁₂₃₇₉, C^'₁₅₈₂₂ und C^'₁₈₈₈₅ Primzahlen.

Weitere Woodall-Primzahlen sind C^'_n für folgende n: 22971, 23005, 98726, 143018, 151023, 667071, 1195203, 1268979, 2013992^[1], 2367906^[2] und 3752948^[3] gefunden durch das BOINC-Projekt PrimeGrid.

Es wird vermutet, dass es unendlich viele Woodall-Primzahlen gibt.

Verallgemeinerte Cullen- und Woodall-Zahlen

Zahlen der Form n · bⁿ + 1 bezeichnet man als verallgemeinerte Cullen-Zahlen. Zahlen der Form n · bⁿ - 1 bezeichnet man als verallgemeinerte Woodall-Zahlen

Weblinks

• Cullen Numbers
• Woodall Numbers
• Bisher bekannte Cullen-Primzahlen
• Bisher bekannte Woodall-Primzahlen

Einzelnachweise

1. ↑ http://www.primegrid.com/download/Woodall2013992.pdf
2. ↑ http://www.primegrid.com/download/Woodall2367906.pdf
3. ↑ http://www.primegrid.com/download/Woodall3752948.pdf

Literatur

• J. Cullen, "Question 15897," Educ. Times, (December 1905) 534.