Schulze-Methode

Dieser Artikel wurde aufgrund von inhaltlichen Mängeln auf der Qualitätssicherungsseite der Redaktion Informatik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Informatik auf ein akzeptables Niveau zu bringen. Hilf mit, die inhaltlichen Mängel dieses Artikels zu beseitigen und beteilige dich an der Diskussion! (+)
Begründung: Bitte wenigstens die Einleitung allgemeinverständlicher machen, vgl. QS-DS --Okmijnuhb·bitte recht freundlich 15:17, 23. Jul. 2011 (CEST)

Die Schulze-Methode (nach Markus Schulze) ist ein Wahlverfahren. Es ist die derzeit verbreitetste Methode, um Wahlen durchzuführen, bei welchen der Wähler Kandidaten nach Rang ordnet (sog. Condorcet-Methode nach Marquis de Condorcet).

Markus Schulze hat die Methode 1997 entwickelt. Die ersten Veröffentlichungen datieren von 2003 und 2006 ^[1][2][3]. Verwendet wurde die Schulze-Methode erstmals 2003 (von Software in the Public Interest), 2003 (von Debian) und 2005 (von Gentoo).

Erklärung

Jeder Wähler erhält eine komplette Liste aller Kandidaten. Er reiht die Kandidaten, indem er Zahlen an die Kandidaten schreibt. Eine kleine Zahl ist besser als eine größere, jedoch zählt nur die Reihenfolge. Kandidaten mit gleicher Zahl sind an gleicher Stelle gereiht. Kandidaten ohne Zahl sind gemeinsam an letzter Stelle – so als ob die größte Zahl bei ihnen geschrieben wurde.

Anzahl der Wähler

Die Anzahl der Wähler, die den Kandidaten A dem Kandidaten B strikt vorziehen, wird durch d[A,B] ausgedrückt.

Definition

Die Schulze-Methode ist folgendermaßen definiert:

Ein Weg (path) vom Kandidaten X zum Kandidaten Y der Stärke z ist eine Sequenz von Kandidaten C(1),…,C(n) mit den folgenden Eigenschaften:

1. C(1) ist identisch mit X.
2. C(n) ist identisch mit Y.
3. Für alle i = 1,…,(n-1): d[C(i),C(i+1)] > d[C(i+1),C(i)].
4. Für alle i = 1,…,(n-1): d[C(i),C(i+1)] ≥ z.
5. Für mindestens ein i = 1,…,(n-1): d[C(i),C(i+1)] = z.

Hat ein Weg C(1),…,C(n) die Stärke z, so werden die Bögen dieses Weges, für die d[C(i),C(i+1)] = z gilt, „kritische Siege“ genannt.

p[A,B], die Stärke des stärksten Weges vom Kandidaten A zum Kandidaten B, ist der größte Wert, so dass es einen Weg dieser Stärke vom Kandidaten A zum Kandidaten B gibt. p[A,B] : = 0, falls es keinen Weg vom Kandidaten A zum Kandidaten B gibt.

Kandidat D ist besser als Kandidat E, genau dann wenn p[D,E] > p[E,D] ist.

Kandidat D ist ein potentieller Sieger, genau dann wenn p[D,E] ≥ p[E,D] ist für jeden anderen Kandidaten E.

Es lässt sich zeigen, dass die „besser“-Relation transitiv ist. Es existiert somit stets mindestens ein potentieller Sieger.

Beispiel 1

Beispiel (45 Wähler; 5 Kandidaten):

(Notation: #Anzahl der Personen, die folgende Reihenfolge der Kandidaten gewählt haben: Kandidat mit höchster Bevorzugung … Kandidat mit niedrigster Bevorzugung)

5 ACBED

5 ADECB

8 BEDAC

3 CABED

7 CAEBD

2 CBADE

7 DCEBA

8 EBADC

Paarweise Matrix

Tabelle, die jeden Kandidaten mit jedem anderen vergleicht. Die rot markierten Felder werden weiter benutzt. Z. B. wurde Kandidat B von 25 Stimmen gegenüber Kandidat A bevorzugt.

	d[*,A]	d[*,B]	d[*,C]	d[*,D]	d[*,E]
d[A,*]		20	26	30	22
d[B,*]	25		16	33	18
d[C,*]	19	29		17	24
d[D,*]	15	12	28		14
d[E,*]	23	27	21	31

Paarweiser Graph

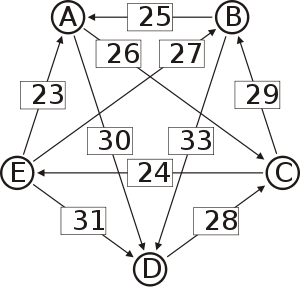
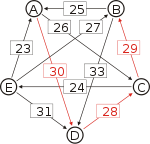
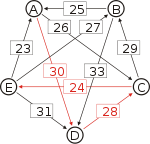
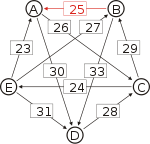
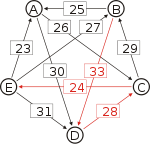
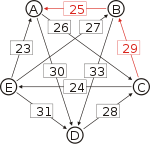
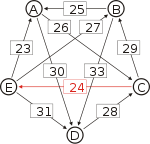
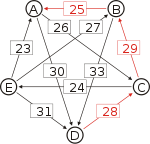
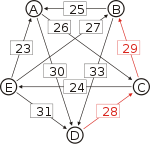
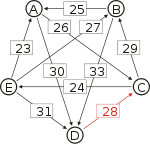
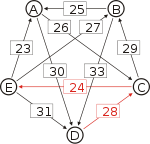
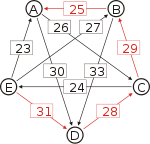
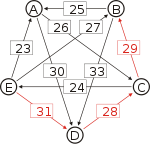
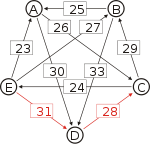
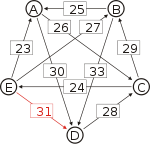
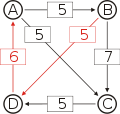
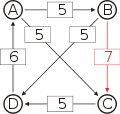
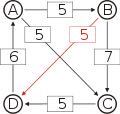
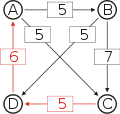
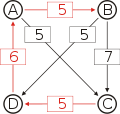
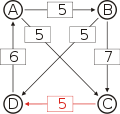
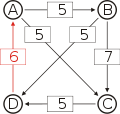
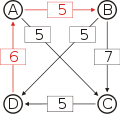
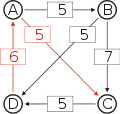
Graph mit gewichteten Pfeilen aus der Tabelle von oben. Man sieht den Pfeil von Kandidat B zu Kandidat A mit dem Gewicht aus der obigen Tabelle, 25.

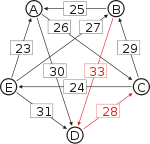
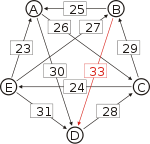
Die stärksten Wege

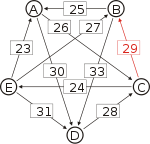
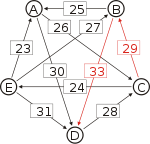
Von den Verbindungen zwischen Kandidaten wird diejenige gesucht, wo das schwächste Glied am stärksten ist. Bildlich gesprochen wird die stärkste Kette gesucht. Wie kommt man von A nach B?

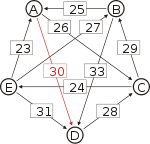
• von A nach C nach B, das schwächste Glied ist von A nach C mit 26.
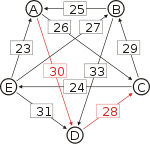
• von A nach D nach C nach B, das schwächste Glied ist D nach C mit 28. Diese Kette ist stärker und die 28 werden weiterverwendet.

Oft wird dieses schwächste Glied der stärksten Kette auch „kritischer Sieg“ genannt. Sie sind hier unterstrichen.

	… nach A	… nach B	… nach C	… nach D	… nach E
von A …		A-(30)-D-(28)-C-(29)-B	A-(30)-D-(28)-C	A-(30)-D	A-(30)-D-(28)-C-(24)-E
von B …	B-(25)-A		B-(33)-D-(28)-C	B-(33)-D	B-(33)-D-(28)-C-(24)-E
von C …	C-(29)-B-(25)-A	C-(29)-B		C-(29)-B-(33)-D	C-(24)-E
von D …	D-(28)-C-(29)-B-(25)-A	D-(28)-C-(29)-B	D-(28)-C		D-(28)-C-(24)-E
von E …	E-(31)-D-(28)-C-(29)-B-(25)-A	E-(31)-D-(28)-C-(29)-B	E-(31)-D-(28)-C	E-(31)-D

Die Stärken der stärksten Wege

Das schwächste Glied der stärksten Verbindung wie oben gefunden, wird in eine Tabelle eingetragen. Dann wird wieder paarweise verglichen, wer wen schlägt, in der Tabelle unten wieder rot markiert.

	p[*,A]	p[*,B]	p[*,C]	p[*,D]	p[*,E]
p[A,*]		28	28	30	24
p[B,*]	25		28	33	24
p[C,*]	25	29		29	24
p[D,*]	25	28	28		24
p[E,*]	25	28	28	31

Ergebnis

Sieger nach der Schulze-Methode ist Kandidat E, da p[E,X] ≥ p[X,E] ist für jeden anderen Kandidaten X.

• Wegen 25 = p[E,A] > p[A,E] = 24 ist Kandidat E besser als Kandidat A.
• Wegen 28 = p[E,B] > p[B,E] = 24 ist Kandidat E besser als Kandidat B.
• Wegen 28 = p[E,C] > p[C,E] = 24 ist Kandidat E besser als Kandidat C.
• Wegen 31 = p[E,D] > p[D,E] = 24 ist Kandidat E besser als Kandidat D.
• Wegen 28 = p[A,B] > p[B,A] = 25 ist Kandidat A besser als Kandidat B.
• Wegen 28 = p[A,C] > p[C,A] = 25 ist Kandidat A besser als Kandidat C.
• Wegen 30 = p[A,D] > p[D,A] = 25 ist Kandidat A besser als Kandidat D.
• Wegen 29 = p[C,B] > p[B,C] = 28 ist Kandidat C besser als Kandidat B.
• Wegen 29 = p[C,D] > p[D,C] = 28 ist Kandidat C besser als Kandidat D.
• Wegen 33 = p[B,D] > p[D,B] = 28 ist Kandidat B besser als Kandidat D.

Das Schulze-Ranking ist somit E > A > C > B > D.

Beispiel 2

Beispiel (9 Wähler; 4 Kandidaten):

3 ABCD

2 DABC

2 DBCA

2 CBDA

Paarweise Matrix

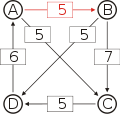
	d[*,A]	d[*,B]	d[*,C]	d[*,D]
d[A,*]		5	5	3
d[B,*]	4		7	5
d[C,*]	4	2		5
d[D,*]	6	4	4

Paarweiser Graph

Die stärksten Wege

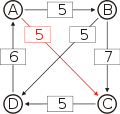
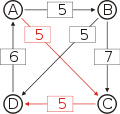
Die kritischen Siege der stärksten Wege sind unterstrichen.

	... nach A	... nach B	... nach C	... nach D
von A ...		A-(5)-B	A-(5)-C	A-(5)-C-(5)-D
von B ...	B-(5)-D-(6)-A		B-(7)-C	B-(5)-D
von C ...	C-(5)-D-(6)-A	C-(5)-D-(6)-A-(5)-B		C-(5)-D
von D ...	D-(6)-A	D-(6)-A-(5)-B	D-(6)-A-(5)-C

Die Stärken der stärksten Wege

	p[*,A]	p[*,B]	p[*,C]	p[*,D]
p[A,*]		5	5	5
p[B,*]	5		7	5
p[C,*]	5	5		5
p[D,*]	6	5	5

Ergebnis

Potentielle Sieger nach der Schulze-Methode sind somit Kandidat B und Kandidat D, da (1) p[B,X] ≥ p[X,B] ist für jeden anderen Kandidaten X und (2) p[D,Y] ≥ p[Y,D] ist für jeden anderen Kandidaten Y.

Wegen 7 = p[B,C] > p[C,B] = 5 ist Kandidat B besser als Kandidat C.

Wegen 6 = p[D,A] > p[A,D] = 5 ist Kandidat D besser als Kandidat A.

Mögliche Schulze-Rankings sind somit B > C > D > A, B > D > A > C, B > D > C > A, D > A > B > C, D > B > A > C und D > B > C > A.

Implementierung

Sei C die Anzahl der Kandidaten. Dann lassen sich die Stärken der stärksten Wege mit Hilfe des Algorithmus von Floyd und Warshall berechnen.

Input: d[i,j] ist die Anzahl der Wähler, die den Kandidaten i dem Kandidaten j strikt vorziehen.

Output: p[i,j] ist die Stärke des stärksten Weges vom Kandidaten i zum Kandidaten j.

Beispiel einer Implementierung in Pascal

for i : = 1 to C
begin
   for j : = 1 to C
   begin
      if ( i ≠ j ) then
      begin
         if ( d[i,j] > d[j,i] ) then
         begin
            p[i,j] : = d[i,j]
         end
         else
         begin
            p[i,j] : = 0
         end
      end
   end
end
 
for i : = 1 to C
begin
   for j : = 1 to C
   begin
      if ( i ≠ j ) then
      begin
         for k : = 1 to C
         begin
            if ( i ≠ k ) then
            begin
               if ( j ≠ k ) then
               begin
                  p[j,k] : = max ( p[j,k], min ( p[j,i], p[i,k] ) )
               end
            end
         end
      end
   end
end

Heuristiken und Eigenschaften

Spezielle Heuristiken der Schulze-Methode sind auch bekannt unter den Namen Beatpath, Beatpaths, Beatpath Method, Beatpath Winner, Path Voting, Path Winner, Schwartz Sequential Dropping (SSD) und Cloneproof Schwartz Sequential Dropping (CSSD).

Die Schulze-Methode erfüllt die folgenden Kriterien^[4][5]:

1. Majority criterion
2. Mutual majority criterion
3. Monotonicity criterion (auch bezeichnet als non-negative responsiveness, mono-raise)
4. Pareto criterion
5. Condorcet-Kriterium
6. Condorcet-Verlierer-Kriterium
7. Smith criterion (auch bezeichnet als Generalized Condorcet criterion)
8. Local independence from irrelevant alternatives
9. Schwartz-Kriterium
10. Strategy-Free criterion
11. Generalized Strategy-Free criterion
12. Strong Defensive Strategy criterion
13. Weak Defensive Strategy criterion
14. Summability criterion
15. Independence of clones
16. nicht-diktatorisch
17. Universalität
18. Woodall's plurality criterion
19. Woodall's CDTT criterion
20. Minimal Defense criterion
21. Resolvability
22. Reversal symmetry
23. mono-append
24. mono-add-plump

Anwendungen

Muster für die elektronischen Stimmzettel für die Wahlen zum Kuratorium der Wikimedia Foundation

Die Schulze-Methode wird derzeit nicht in öffentlichen Wahlen angewandt. Sie findet jedoch mehr und mehr Anwendung in Privatorganisationen. Derzeit wird sie in folgenden Organisationen benutzt:

• Wikimedia^[6]
• Piratenpartei Deutschland^[7]
• Piratenpartei Schweden^[8]
• französischsprachige Wikipedia^[9]
• Debian^[10]
• Software in the Public Interest^[11]
• Gentoo Foundation
• Sender Policy Framework^[12]
• Free Software Foundation Europe (FSFE)^[13]
• KDE e.V.^[14]
• Mathematical Knowledge Management Interest Group (MKM-IG)
• Kingman Hall^[15]
• TopCoder
• GNU Privacy Guard^[16]

Siehe auch

• Ranked Pairs
• Sozialwahltheorie
• Condorcet-Paradoxon
• LiquidFeedback

Literatur

• Christoph Börgers, Mathematics of Social Choice: Voting, Compensation, and Division, SIAM 2009, ISBN 0-8987-1695-0
• Saul Stahl und Paul E. Johnson, Understanding Modern Mathematics, Jones & Bartlett Publishing, London u.a. 2007, ISBN 0-7637-3401-2, S. 119ff.
• Nicolaus Tideman, Collective Decisions and Voting: The Potential for Public Choice, Ashgate Publishing 2006, ISBN 0-7546-4717-X, S. 228ff.

Einzelnachweise

1. ↑ Condorect sub-cycle rule, Election Methods Mailing Liste, 3. Oktober 1997
2. ↑ Markus Schulze, A new monotonic and clone-independent single-winner election method, Voting Matters, issue 17, pages 9–19, 2003
3. ↑ Nicolaus Tideman, „Collective Decisions and Voting: The Potential for Public Choice“, Ashgate Publishing, 2006, und Saul Stahl, Paul E. Johnson, „Understanding Modern Mathematics“, Jones & Bartlett Publishing, 2006
4. ↑ A new monotonic, clone-independent, reversal symmetric, and Condorcet-consistent single-winner election method, Markus Schulze, Juli 2007 (PDF, englisch)
5. ↑ Properties of Preferential Election Rules, D. R. Woodall, Dezember 1994 (englisch)
6. ↑ Board election to use preference voting, Mai 2008
7. ↑ Pressererklärung der Piratenpartei Deutschland , August 2010
8. ↑ Probewahl der schwedischen Piraten, Januar 2010
9. ↑ Prise de décision, Dezember 2005
10. ↑ Verfassung für das Debian-Projekt, Anhang A6
11. ↑ Process for adding new board members, Januar 2003
12. ↑ Council Election Procedures
13. ↑ § 6 Absatz 3 der Satzung
14. ↑ Artikel 3.4.1 der Rules of Procedures for Online Voting
15. ↑ Kingman adopts Condorcet voting, April 2005
16. ↑ GnuPG Logo Vote, November 2006

Weblinks

 Commons: Schulze method – Album mit Bildern und/oder Videos und Audiodateien

• Rosa Camps, Xavier Mora und Laia Saumell: A Continuous Rating Method for Preferential Voting (PDF-Datei; 1,76 MB)
• Paul E. Johnson: Voting Systems (PDF-Datei; 324 kB)
• Rob LeGrand: Descriptions of ranked-ballot voting methods.
• Rob Loring: Accurate Democracy.
• James D. McCaffrey: Testlauf: Gruppenentscheidungen bei Softwaretests
• Tommi Meskanen und Hannu Nurmi: Distance from Consensus: a Theme and Variations (PDF-Datei; 130 kB), in: Bruno Simeone, Friedrich Pukelsheim (Hgg.): Mathematics and democracy: recent advances in voting systems and collective choice. Studies in choice and welfare, Springer, Berlin u.a. 2006, ISBN 3540356037, S. 117-132, hier S. 120ff.
• Massimo Narizzano, Luca Pulina und Armando Tacchella: Ranking and Reputation Systems in the QBF Competition, in: AI*IA '07 Proceedings of the 10th Congress of the Italian Association for Artificial Intelligence on AI*IA 2007: Artificial Intelligence and Human-Oriented Computing, Springer, Berlin, Heidelberg 2007, ISBN 978-3-540-74781-9.
• Markus Schulze: Schulze-Methode FAQ
• Markus Schulze: A New Monotonic and Clone-Independent Single-Winner Election Method, in: Voting Matters 17 (2003), S. 9-19 (PDF-Datei; 602 kB).
• Kevin Venzke: Election Methods and Criteria.
• Jochen Voss: The Debian Voting System
• Barry Wright: Objective Measures of Preferential Ballot Voting Systems, Abschlussarbeit Duke University, Durham, North Carolina 2009.