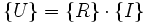- Zugschnittene Größengleichung
-
Die Zahlenwertgleichung ist eine Darstellungsform einer Gleichung, die statt (physikalischer, finanztechnischer usw.) Größen nur ihre Maßzahlen verknüpft. Mit welchen Maßeinheiten sie gültig ist, wird separat angegeben.
Dieses Vorgehen ist systematisch unbefriedigend und nach heute gültigen Konventionen nicht korrekt, aber im praktischen/handwerklichen Bereich immer noch verbreitet.
Inhaltsverzeichnis
Beispiele
Ohm'sches Gesetz
Beispielsweise lautet das ohmsche Gesetz in veralteter Zahlenwertschreibweise:
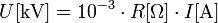 .
.
Diese Schreibweise führt vielfach zu Missverständnissen, da heute die eckigen Klammern um das Formelzeichen geschrieben werden mit der Bedeutung „Einheit von …“. In der veralteten Form der Zahlenwertgleichung wird jedoch die Einheit geklammert.
mechanische Leistungsformel
In der technischen Mechanik sind vielfach von den gebräuchlichen Größen
- Leistung P in [kW] (Kilowatt)
- Drehzahl n in [min-1] (Umdrehungen je Minute)
- Drehmoment M in [Nm] (Newtonmeter)
zwei Werte bekannt.
Die fehlende Größe wird hinreichend genau mit der Zahlenwertgleichung
berechnet.
- Für die Leistung P ergibt sich umgestellt
- Die Drehzahl n ermittelt sich aus
Herleitung
Der gerundete Zahlenwert 9550 ist lediglich eine leicht zu merkende, praxisgerechte Konstante für die physikalisch korrekte Berechnung. Die fehlerträchtigen Umrechnungen der in der technischen Praxis üblichen Einheiten auf physikalisch korrekte Basiseinheiten entfällt. Die Konstante beinhaltet die Umrechnung von Minute in Sekunde, Kilowatt in Watt und die Drehzahl je Minute in die Kreisfrequenz ω (Omega). In der praktischen Anwendung wird vielfach der Wert von π zu 3,1415 gerundet verwendet.
Die technische Schulungsliteratur gibt daher den hinreichend genauen Faktor mit 9550 an.
Größengleichungen
Die Größengleichung der oben genannten Zahlenwertgleichung sieht wie folgt aus:
Möchte man diese Gleichung nur mit Zahlenwerten aufbauen, kann die zugeschnittene Größengleichung verwendet werden, in der die physikalischen Größen durch ihre Einheiten geteilt werden:
Dies folgt aus der Schreibweise einer physikalischen Größe:
(sprich: Die Spannung U ist der Zahlenwert von U mal die Einheit von U)
Zu beachten: es steht das Formelzeichen in der eckigen Klammer, nicht die Einheit selbst, da das Formelzeichen in eckigen Klammern die Einheit selbst darstellt, also [U] = V!
Obige Gleichung nach dem Zahlenwert aufgelöst ergibt:
Daraus folgt direkt die Zahlenwertgleichung in heutiger Form:
also eine Gleichung, die nur aus Zahlen besteht!
Diese Gleichung führt aber nur dann zu einem richtigen Ergebnis, wenn zuvor, wie bereits oben angedeutet, mit den zugehörigen Einheiten gerechnet wurde.
Die oben zuerst angeführte Gleichung sieht demnach als zugeschnittene Größengleichung folgendermaßen aus:
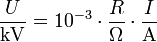 .
.
Es wird jeweils ein Quotient aus der Größe und der gewünschten Einheit geschrieben. Diese Darstellung kann daher so gelesen werden, wie Benutzer der Zahlenwertgleichungen es gewöhnt sind. Sie ist aber nach den heute üblichen Konventionen gültig und verständlich.
Begriff
Die Bezeichnungen „Zahlenwertgleichung“, „Größengleichung“ und „zugeschnittene Größengleichung“ gehen auf Julius Wallot zurück und werden in der Norm DIN 1313 „Physikalische Größen und Gleichungen“ (Erstausgabe 1931: „Schreibweise physikalischer Gleichungen“) behandelt.
Wikimedia Foundation.

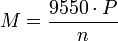
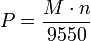
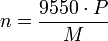
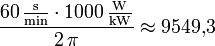
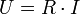
![\frac{U}{\left[ U \right]} = \frac{R}{\left[ R \right]} \cdot \frac{I}{\left[ I \right]}](/pictures/dewiki/53/5d92ac5d0185405cb757b4775d3454e3.png)
![U = \left\{U\right\} \cdot [U]](/pictures/dewiki/50/26bb6d9a925fb6d6e46f0faf744f3766.png)
![\left\{U\right\} = \frac{U}{\left[ U \right]}](/pictures/dewiki/100/d37780112d37214969acc9c166bb8cc9.png)