Bethe-Formel

Die Bethe-Formel gibt den Energieverlust pro Weglängeneinheit an, den schnelle geladene Teilchen (Protonen, Alphateilchen, Atomionen, aber nicht Elektronen^{[Anmerkung 1][1]}) beim Durchgang durch Materie erleiden (bzw. das Bremsvermögen des Materials). Die nicht-relativistische Formel wurde von Hans Bethe 1930 aufgestellt; die unten gezeigte relativistische Version stellte Bethe 1932 auf (Sigmund 2006).

Bewegen sich schnelle geladene Teilchen durch Materie, so wechselwirken sie mit den Hüllenelektronen der Atome des Materials. Diese Wechselwirkung führt zur Anregung oder zur Ionisation der Atome. Dadurch erleidet das durchquerende Teilchen einen Energieverlust, welcher durch die unten angegebene Formel näherungsweise angegeben wird.

Die Formel

Die relativistische Form der Formel lautet:

$- \frac{dE}{dx} = \frac{4 \pi nz^2}{m_{\rm e} c^2 \beta^2 } \cdot \left(\frac{e^2}{4\pi\epsilon_0}\right)^2 \cdot \left[\ln \left(\frac{2m_{\rm e} c^2 \beta^2}{I \cdot (1-\beta^2)}\right) - \beta^2\right]$            (1)

wobei

β	= v / c
v	= Geschwindigkeit des Teilchens
E	= Energie des Teilchens
x	= Weglänge
c	= Lichtgeschwindigkeit
z	= Anzahl der Ladungen des Teilchens ($z\cdot e$ = Ladung des Teilchens)
e	= Elementarladung
n	= Elektronendichte des Materials
me	= Ruhemasse des Elektrons
I	= Mittleres Anregungspotential des Materials (s.u.)

Bremsvermögen von Aluminium für Protonen als Funktion der Energie des Protons, mit Bethe-Formel

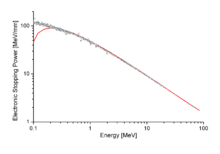
Die Elektronendichte n lässt sich dabei mit $n=\frac{ Z\cdot\rho }{ A\cdot u }$ berechnen. Dabei ist ρ die Dichte des durchdrungenen Materials, Z und A Ordnungs- bzw. Atommassenzahl des Materials und u die atomare Masseneinheit.

Im Bild rechts bedeuten die kleinen Kreise Messergebnisse, die von verschiedenen Arbeitsgruppen aus Messungen gewonnen wurden^[2]; die rote Kurve stellt die Bethe-Formel dar. Offenbar ist die Übereinstimmung von Bethes Theorie mit den Experimenten bei hoher Energie sehr gut. Nur unterhalb von 0,3 MeV liegt die Kurve zu tief; dort fehlen die Korrekturen (s.u.).

Für kleine Energien, d. h. für kleine Teilchengeschwindigkeiten $( \beta \ll 1)$, reduziert sich die Bethe-Formel auf

$- \frac{dE}{dx} = \frac{4 \pi nz^2}{m_e v^2} \cdot \left(\frac{e^2}{4\pi\varepsilon_0}\right)^2 \cdot \left[\ln \left(\frac{2m_e v^2 }{I}\right)\right].$

Für kleine Energien fällt laut Bethe-Formel der Energieverlust bei steigender Energie etwa mit 1 / v² ab und erreicht ein Minimum bei etwa E = 3m_Tc², wobei m_T die Masse des Teilchens ist (also z. B. für Protonen etwa bei 3000 MeV, was im Bild nicht mehr sichtbar ist). Im stark relativistischen Bereich $( \beta \approx 1)$ steigt der Energieverlust wieder logarithmisch an. Da für viele in der Teilchenphysik relevante Strahlungsteilchen und Absorbermaterialien der Energieverlust in der Nähe des Minimums in etwa den gleichen Wert hat, werden Teilchen mit einer Energie in der Nähe des Minimums häufig zusammengefasst und als MIPs (Minimal Ionizing Particles - Minimal ionisierende Teilchen) bezeichnet. Als Faustformel für den spezifischen Energieverlust der MIPs gilt:

$-\frac{1}{\rho}\frac{\mathrm d E}{\mathrm d x}\approx 1{,}5 \frac{\mathrm{MeV}}{\mathrm g\;\mathrm{cm}^{-2}}$.

Bei noch höheren Energien müssen auch die Teilchenreaktionen berücksichtigt werden, die aufgrund der hohen kinetischen Energie des Strahlungsteilchens zu Sekundärteilchen führen. Der Energieverlust kann daher noch weiter ansteigen, hängt dann aber teilweise wieder vom Material ab.

Bei kleinen Energien ist die Bethe-Formel nur dann gültig, wenn diese so hoch sind, dass das ionisierende und auch selbst geladene und ionisierte Teilchen keinerlei Hüllenelektronen mehr mit sich führt. Wenn das ionisierende Teilchen noch Elektronen mit sich führt, wird die effektive Teilchenladung dadurch reduziert, und das Bremsvermögen ist kleiner. Auch wenn das atomare Teilchen vollständig ionisiert ist, ist die Bethe-Formel jedoch nur eine Näherungsgleichung, so dass für eine höhere Genauigkeit noch Korrekturen notwendig sind (s.u.).

Das mittlere Anregungspotential

Im Gültigkeitsbereich der Bethe-Formel (1) wird das durchdrungene Material durch eine einzige Konstante, das mittlere Anregungspotential I, beschrieben.

Felix Bloch hat 1933 gezeigt, dass das mittlere Anregungspotential der Atome im Mittel etwa

$I = (10eV) \cdot Z$           (2)

beträgt, wo Z die Ordnungszahl der Atome des Materials bedeutet. Setzt man diese Größe in Formel (1) oben ein, so führt das zu einer Gleichung, die oft als Bethe-Bloch-Gleichung bezeichnet wird. Da es aber genauere Tabellen von I als Funktion von Z gibt (z. B. im ICRU Report 49 der International Commission on Radiation Units and Measurements, „Stopping Powers and Ranges for Protons and Alpha Particles“, 1993), erhält man durch Verwendung einer solchen Tabelle bessere Resultate als mit Formel (2).

Das mittlere Anregungspotential I von Elementen, dividiert durch die Ordnungszahl Z, aufgetragen über der Ordnungszahl

Im Bild links ist das mittlere Anregungspotential der verschiedenen Elemente gezeigt, das die Information über das jeweilige Atom enthält. Die Daten stammen aus dem ICRU Report 49. Den Spitzen und Tälern in der Darstellung („Z₂-Oszillationen“, wobei Z₂ = Z die Ordnungszahl des Materials bedeutet) entsprechen niedrigere bzw. höhere Werte des Bremsvermögens; diese Oszillationen beruhen auf der Schalenstruktur der Elemente. Wie das Bild zeigt, gilt Formel (2) nur näherungsweise.

Zum Namen der Formel

Die Bethe-Formel wird manchmal auch als Bethe-Bloch-Formel bezeichnet, was aber irreführend ist.

In der Beschreibung der Programme PSTAR und ASTAR (für Protonen und Alphateilchen), die das National Institute of Standards and Technology (NIST) zur Verfügung stellt, heißt die Formel (1) sinnvollerweise "Bethe's stopping power formula"^[3].

In der 2006 edition of Review of Particle Physics ^[4] anderseits heißt die Formel unlogischerweise "Bethe-Bloch equation", obwohl dort der Blochsche Ausdruck (2) gar nicht vorkommt.

Korrekturen zur Bethe-Formel

Die Bethe-Formel wurde von Bethe mit Hilfe der quantenmechanischen Störungstheorie abgeleitet, das Ergebnis ist daher dem Quadrat der Ladung z proportional. Eine bessere Beschreibung erhält man, wenn man auch Abweichungen berücksichtigt, die höheren Potenzen von z entsprechen, und zwar den Barkas-Andersen-Effekt (proportional z³; nach Walter H. Barkas und Hans Henrik Andersen) und die Bloch-Korrektur (proportional z⁴; nach Felix Bloch). Außerdem ist es notwendig, die Bewegung der Hüllenelektronen im Atom des Materials zu berücksichtigen („Schalenkorrektur“).

Diese Korrekturen sind beispielsweise in den Programmen PSTAR und ASTAR des National Institute of Standards and Technology (NIST), die das Bremsvermögen für Protonen bzw. Alphateilchen berechnen, eingebaut.^[5] Die Korrekturen sind groß bei niedrigen Energien und werden immer kleiner, je größer die Energie wird.

Zusätzlich kommt bei sehr hohen Energien noch Fermis Dichtekorrektur^[6] hinzu.

Literatur

• Sigmund P.: Particle Penetration and Radiation Effects, General Aspects and Stopping of Swift Point Charges, Springer Series in Solid State Sciences Vol. 151, Springer-Verlag Berlin Heidelberg (2006), ISBN 978-3-540-72622-7

Quellen

1. ↑ H. Bethe und J. Ashkin in "Experimental Nuclear Physics, ed. E. Segré, J. Wiley, New York, 1953, p. 253
2. ↑ Bildquelle www.exphys.uni-linz.ac.at/Stopping/
3. ↑ Description of PSTAR and ASTAR databases
4. ↑ W-M Yao et al. 2006 J. Phys. G: Nucl. Part. Phys. 33 1–1232
5. ↑ PSTAR and ASTAR Databases for Protons and Helium Ions
6. ↑ ICRU Report 49, International Commission on Radiation Units and Measurements, Bethesda, MD, USA (1993)

Anmerkung

1. ↑ Für Elektronen ist der Energieverlust etwas anders wegen ihrer geringen Masse und der Ununterscheidbarkeit, und weil sie viel stärkere Verluste durch Bremsstrahlung erleiden

Weblinks

• Ursprüngliche Publikation von Bethe in „Annalen der Physik“, 1930
• Durchgang geladener Teilchen durch Materie, inklusive Plot (engl.; PDF-Datei; 512 kB)
• Bremsvermögen für Protonen und Alphateilchen (engl.)
• Stopping Power Daten und Kurven (engl.)