Bremsvermögen

Bremsvermögen von Aluminium für Protonen als Funktion der Energie des Protons.

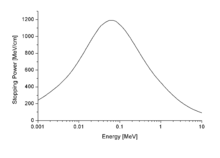
Beim Durchgang durch Materie ionisieren geladene Teilchen die Atome oder Moleküle, auf die sie treffen. Dabei verlieren sie schrittweise Energie. Mit Bremsvermögen des Materials (englisch: Stopping Power) bezeichnet man den Energieverlust pro Weglängeneinheit der Teilchen, gemessen beispielsweise in MeV/cm (siehe Bild).

Bremsvermögen, Bragg-Peak und Reichweite

Das Bremsvermögen ist abhängig von der Teilchenart, vom Material und von der augenblicklichen Energie. Da die Erzeugung eines Ionenpaares eine bestimmte Energiemenge kostet (in Luft z. B. 34 eV), ist die Ionisationsdichte längs der Teilchenbahn proportional zum Energieverlust pro Weglängeneinheit.

Sowohl Elektronen als auch Mesonen und positive Ionen verlieren Energie beim Durchgang durch Materie. Im folgenden betrachten wir vor allem positive Ionen.

Der Ausdruck Bremsvermögen beschreibt die Situation sozusagen vom Standpunkt des bremsenden Materials aus, während Energieverlust pro Weglängeneinheit sich auf das Teilchen bezieht. In Bezug auf Einheit und Zahlenwert sind beide Größen identisch. Der Energieverlust pro Weglängeneinheit wird üblicherweise mit negativem Vorzeichen geschrieben:

$S(E) = -{dE \over dx}$

wobei E die Energie und x die Weglänge bedeutet. Infolge des Minuszeichens ist S eine positive Größe. Meistens steigt der Energieverlust pro Wegeinheit während des Weges, den das Teilchen zurücklegt, an. Die Kurve, die dies beschreibt, heißt Bragg-Kurve.

Braggkurve von 5.49 MeV Alphateilchen in Luft

Kurz vor dem Ende des Weges durchläuft der Energieverlust ein Maximum (Bragg-Peak, benannt nach William Henry Bragg) und fällt dann abrupt auf (fast) Null ab. Dies ist von großer praktischer Bedeutung bei der Strahlentherapie.

Die obige Gleichung beschreibt das lineare Bremsvermögen, das in Einheiten wie zum Beispiel MeV/mm gemessen wird. Dividiert man das lineare Bremsvermögen durch die Dichte des Materials, so erhält man das Massenbremsvermögen, das in Einheiten wie beispielsweise MeV/(mg/cm²) gemessen wird. Das Massenbremsvermögen ist unabhängig von der Materialdichte.

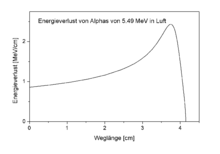
Das Bild zeigt, wie der Energieverlust pro Weglängeneinheit (die Stopping Power) - und damit die Ionisationsdichte - der Alphateilchen während des Weges in Luft zunimmt, bis sie das Maximum erreicht. Die Energie von 5.49 MeV entspricht der des natürlichen Radongases (Radon-222), das überall vorkommt, wo es Granit im Boden gibt. Die Darstellung hier unterscheidet sich von der im Bild oben dadurch, dass hier die Teilchen eine fixe Anfangsenergie haben.

Der Weg, den die Teilchen zurücklegen, bis ihre Energie auf Null sinkt, heißt Reichweite. Die Reichweite ist abhängig von der Teilchenart, von der Anfangsenergie und von dem Material, das die Teilchen durchqueren. Man kann die Reichweite berechnen, indem man das reziproke Bremsvermögen über die Energie (von der Anfangsenergie bis Null) integriert.

Braggkurven und Photonenabsorption

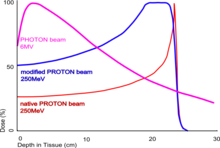
Das dritte Bild zeigt die Energiedeposition eines Protonenstrahls von 250 MeV, in Wasser (orangefarbene Kurve); die Kurve hat einen sehr spitzen Bragg-Peak. Die blaue Kurve zeigt die gesamte Energiedeposition bei mehreren aufeinanderfolgenden Implantionen mit variierenden Energien. Solche Protonenstrahlen werden bei der Strahlentherapie genutzt um ausgedehnte Tumore zu bestrahlen, da hierbei der größte Teil der Energiedeposition und damit auch der Schädigung im Tumor selbst stattfindet.

Das Bild zeigt zum Vergleich auch die Absorption eines hochenergetischen Photonenstrahls. Diese Kurve ist gänzlich anders (im Wesentlichen eine exponentielle Abnahme), da das Photon nicht allmählich durch viele Ionisationen Energie abgibt, sondern meist in einem einzigen Ionisationsprozess seine ganze Energie verliert (siehe auch Teilchenstrahlung). Die Absorption eines Photonenstrahls wird nicht durch das Bremsvermögen beschrieben, sondern durch einen Absorptionskoeffizienten.

Die englischen Ausdrücke Stopping Power und Bragg-Peak sind auch im Deutschen sehr üblich.

Elektronisches und nukleares Bremsvermögen

Unter elektronischem Bremsvermögen versteht man die Abbremsung durch inelastische Stöße zwischen dem schnellen Ion und den Elektronen des durchquerten Mediums. Diese Stöße können sowohl zu Anregung und Ionisation der Elektronen des Mediums als auch der Elektronen des Ions führen.

Mit einer Genauigkeit von einigen Prozent kann man das elektronische Bremsvermögen oberhalb einer Energie von einigen hundert keV theoretisch berechnen, beispielsweise durch die Bethe-Formel. Für niedrigere Energien wird die Berechnung schwieriger.^[1]

Graphische Darstellungen der experimentellen Werte des elektronischen Bremsvermögens für viele Ionen in vielen verschiedenen Substanzen findet man in ^[2]. Die Genauigkeit verschiedener Tabellen zum Bremsvermögen wurde mit Hilfe statistischer Methoden untersucht u.a. von H. Paul^[3]

Elektronisches und nukleares Bremsvermögen von Aluminium für Aluminiumionen, über der Teilchenenergie. Das Maximum des nuklearen Bremsvermögens liegt typisch bei Energien von etwa 1 keV pro Nukleon, des elektronischen Bremsvermögens oberhalb von 100 keV pro Nukleon

Unter nuklearem Bremsvermögen versteht man elastische Stöße zwischen dem Ion und den Atomen des Materials (der übliche Ausdruck "nuklear" hat aber nichts mit nuklearen Kräften, also Kernkräften zu tun). Wenn man die Form des abstoßenden Potentials V(r) zwischen Ion und Atom kennt, kann man das nukleare Bremsvermögen S_n(E) berechnen. In dem oben gezeigten Bild für Protonen in Aluminium ist der nukleare Beitrag überall vernachlässigbar, außer bei der kleinsten Energie. Mit steigender Masse des Ions wächst aber der nukleare Beitrag. In der hier rechts gezeigten Figur ist bei kleiner Energie der nukleare Beitrag größer als der elektronische.

Bei nicht zu hohen Energien ist das Bremsvermögen daher die Summe zweier Größen: S(E) = S_e(E) + S_n(E). Es gibt verschiedene semi-empirische Modelle zur Berechnung des Bremsvermögens. Das Modell von Ziegler, Biersack und Littmark wurde ursprünglich in dem Buch ^[4] beschrieben. Die neueste Version des Programms, die man unter ^[5] findet, wird heute sehr viel verwendet.

Literaturzitate

1. ↑ P. Sigmund, Particle Penetration and Radiation Effects. Springer Berlin Heidelberg New York, 2005
2. ↑ H.Paul: http://www.exphys.uni-linz.ac.at/Stopping/
3. ↑ H.Paul: A comparison of recent stopping power tables for light and medium-heavy ions with experimental data, and applications to radiotherapy dosimetry, Nucl. Instrum. Methods Phys. Res. B 247 (2006) 166
4. ↑ J. F. Ziegler, J. P. Biersack, and U. Littmark, The Stopping and Range of Ions in Matter, volume 1, Pergamon, New York, 1985.
5. ↑ J.F.Ziegler: http://www.SRIM.org

Weblinks

• Durchgang geladener Teilchen durch Materie, inklusive Plot (engl.; PDF-Datei; 512 kB)

• Bremsvermögen für Protonen und Alphateilchen (engl.)

• Stopping Power: Daten und Kurven (engl.)