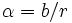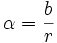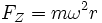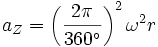Bogenwinkel

Das Bogenmaß ist ein Winkelmaß. Die dimensionslose Zahl trägt oft den Zusatz Radiant bzw. rad, um die Größe von Grad zu unterscheiden.

Umrechnung

Für die Umrechnung vom Bogenmaß ins Gradmaß siehe Umrechnung zwischen Radiant und Grad.

Die Umrechnungsfunktion von Winkel im Gradmaß in das Bogenmaß heißt arc oder arcus (lat. Bogen). Somit ist arc(α) das Bogenmaß des in Grad angegebenen Winkels α.

Die Angaben Bogenminute und Bogensekunde beziehen sich nicht auf das Bogenmaß, sondern sind Untereinheiten von Grad.

Definition

Das Bogenmaß, Definition am Kreissektor: $\alpha = b/r\,$

Das Bogenmaß eines Winkels α (aufgefasst als Zentriwinkel eines Kreises) ist definiert als das Verhältnis der Länge des Kreisbogens b zum Radius r:

$\alpha = \frac{b}{r} \,$

Ist der Kreis ein Einheitskreis (Radius r = 1), so ist das Bogenmaß gleich der Länge des Kreisbogens b.

Um auf die Verwendung des Bogenmaßes hinzuweisen, kann der Maßzahl die Hilfsmaßeinheit Radiant mit dem Einheitenzeichen „rad“ nachgestellt werden. Dabei ist 1 rad die Größe desjenigen Winkels, der einen Bogen b mit der Länge des Radius r ergibt, also b = r. Da das Verhältnis von Kreisumfang zu Radius = 2π. beträgt, beträgt der Vollwinkel (360°) im Bogenmaß 2π rad.

In vielen Berechnungen der Physik und der Mathematik ist das Bogenmaß das zweckmäßigste Winkelmaß. Für den Alltagsgebrauch ist es unpraktisch, da Werte im Bogenmaß recht unanschaulich sind (z.B. hat ein Winkel mit dem Bogenmaß 1 rad ein Gradmaß von ca. 57°). Daher wird in der Alltagspraxis stattdessen meist das Gradmaß verwendet.

Das Bogenmaß in der Physik

In der Physik tritt das Bogenmaß beispielsweise bei der Berechnung der Zentripetalkraft und der Zentrifugalkraft auf. Die Zentripetalkraft beträgt

$F_Z=m \omega^2r \,$

und die Zentripetalbeschleunigung

$a_Z=\omega^2 r \,$,

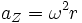wobei 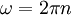$\omega = 2\pi n\;$ die Winkelgeschwindigkeit in rad/s bei der Drehzahl n ist. In dieser Formel ist das Bogenmaß die zweckmäßigste Winkeleinheit für die Winkelgeschwindigkeit; würde man 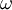$\omega\;$ anstelle im Bogenmaß beispielsweise in Grad pro Sekunde angeben, so würde die Formel

$a_Z=\left(\frac{2\pi}{360^\circ}\right)^2\omega^2 r \,$

lauten; es wären dann also zusätzliche Umrechnungsfaktoren zu berücksichtigen.

Das Bogenmaß in der Mathematik

Winkelfunktionen

In der Mathematik tritt das Bogenmaß insbesondere bei den Winkelfunktionen Sinus und Kosinus auf. Für die Ableitungen dieser Funktionen gilt

$\sin^\prime x = \frac{2\pi}{c}\cos x \,$,

$\cos^\prime x = -\frac{2\pi}{c}\sin x \,$,

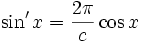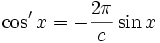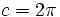wobei die Konstante $c\;$ das Winkelmaß des vollen Kreises, also 360° im Gradmaß oder 400 gon im Gonmaß ist. Misst man im Bogenmaß, so ist $c=2\pi\;$, der Faktor ist 1, und die Formeln vereinfachen sich zu

$\sin^\prime x = \cos x \,$

$\cos^\prime x = -\sin x \,$.

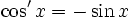Aus diesem Grund wird in der Differentialrechnung der Winkel ausschließlich im Bogenmaß gemessen.

Siehe auch

• Winkelmaß
• Zeitmaß
• Gon
• Kreissektor

Weblinks

• Das Bogenmaß und seine Umwandlung