Zentripetalkraft

Zentripetalkraft

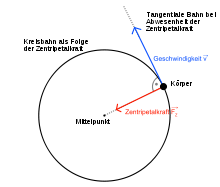
Die Zentripetalkraft (auch Radialkraft) ist die physikalische Kraft, die auf einen Körper wirken muss, damit sich dieser auf einer gekrümmten Bahnkurve bewegt.

Ohne diese Kraft würde sich der Körper nach dem Trägheitsgesetz gleichförmig in Richtung des momentanen Geschwindigkeitsvektors (dem Tangentialvektor der Kurve) bewegen. Die Zentripetalkraft zeigt zum Mittelpunkt des Krümmungskreises und steht damit senkrecht auf dem Geschwindigkeitsvektor.

Zentripetalkraft und Zentralkraft

Während eine Zentralkraft stets auf den gleichen Punkt gerichtet ist, zeigt die Zentripetalkraft zum Mittelpunkt des momentanen Krümmungskreises. Nur bei einer reinen Kreisbewegung ist die Zentripetalkraft eine Zentralkraft.

Beispiele

• Wenn ein Auto eine Kurve durchfährt, ist dies nur dadurch möglich, dass eine zur Innenseite der Kurve gerichtete Zentripetalkraft wirkt. Sie ergibt sich aus der Summe der Seitenkräfte die zwischen Reifen und Fahrbahn entstehen und auf das Fahrzeug einwirken. Fehlt diese Kraft (z. B. bei Glatteis), so bewegt sich das Auto geradlinig weiter, wird also aus der Kurve getragen. Der Fahrzeuginsasse bewegt sich auf der gleichen Kreisbahn wie das Auto, weil der Sitz auf ihn eine Zentripetalkraft ausübt.
• Die Erde bewegt sich (annähernd) auf einer Kreisbahn um die Sonne. Diese Kreisbewegung wird durch die von der Sonne auf die Erde ausgeübte Gravitationskraft verursacht, die dabei als Zentripetalkraft dient. Genau genommen ist die Erdbahn wie die Bahnen aller Planeten keine Kreisbahn, sondern eine Ellipsenbahn. Die Gravitation zeigt als Zentralkraft auf die Sonne, die sich in einem der Ellipsenbrennpunkte befindet. Diese Zentralkraft weicht jedoch leicht von der Zentripetalkraft ab, die zum Zentrum der lokalen Bahnkrümmung zeigt. Die Differenz zwischen Zentralkraft und Zentripetalkraft ist eine Tangentialkomponente, die dafür sorgt, dass der Planet sich in Sonnennähe (im Perihel) schneller bewegt als in Sonnenferne.
• Bewegen sich Elektronen senkrecht zu einem homogenen Magnetfeld, so werden sie durch die Lorentzkraft senkrecht zur Richtung der Bewegung und des Magnetfelds in eine Kreisbahn abgelenkt. In diesem Beispiel ist also die Lorentzkraft die Zentripetalkraft.
• Bei Luftwirbeln ist die Zentripetalkraft der Druckgradient, d. h. im Wirbelkern herrscht Unterdruck.

Etymologie und Begriffsgeschichte

Der Begriff Zentripetalkraft leitet sich von petere (lateinisch für streben nach, sich begeben) ab. Er wurde als vis centripeta von Isaac Newton eingeführt. Newton verwendete den Begriff allerdings nicht im heutigen Sinne, sondern im Sinne einer anziehenden Zentralkraft.^[1] Den Namen prägte Newton als Gegensatz zu der von Christian Huygens zuvor eingeführten Zentrifugalkraft.^[2][3]

Formeln

Die Zentripetalkraft zeigt bei einer Kreisbewegung zum Kreismittelpunkt. Für einen Körper der Masse m, mit der Geschwindigkeit v auf einer Kreisbahn mit Radius r ist der Betrag der Zentripetalkraft:

$F_Z=\frac{m \cdot v^2}{r}$

Mit der Winkelgeschwindigkeit ω ergibt sich die Bahngeschwindigkeit als v = ωr und damit:

$\,F_Z=m \omega^2r$

Verwendet man die Vektoren $\vec{r}$ für den Abstand und $\vec{\omega}$ für die Winkelgeschwindigkeit, so kann man die Zentripetalkraft mit dem Vektorprodukt darstellen:

$\vec{F_Z}= m \vec{\omega} \times (\vec{\omega} \times \vec{r})$

In den Formeln taucht die Masse m als Faktor auf. Wegen der Beziehung „Kraft = Masse · Beschleunigung“ kann daraus die Zentripetalbeschleunigung für einen Körper auf einer Kreisbahn bestimmt werden:

$a_Z=\frac{v^2}{r}$

bzw. mit der Winkelgeschwindigkeit ω:

$a_Z=\omega^2 \cdot r$

Eine allgemeiner gültige Definition ist:

$\vec{a_Z} = \vec{\omega} \times ( \vec{\omega} \times \vec{r})$

Oder durch Umformen mit der Graßmann-Identität:

$\vec{a_Z} = \vec{\omega} ( \vec{\omega} \cdot \vec{r} ) - |\vec{\omega} |^2 \vec{r}$

Im allgemeinen Fall einer beliebigen Kurve gilt die gleiche Formel für die Zentripetalbeschleunigung, nur ist für die Krümmung der lokale Krümmungsradius der Kurve einzusetzen und die Beschleunigung ist zum lokalen Krümmungsmittelpunkt der Kurve gerichtet.

Einzelnachweise

1. ↑ Principia, Definition 5 am Anfang des Werks
2. ↑ I. Bernard Cohen: Newtons Third Law and Universal Gravity. In: Paul B. Scheurer, G. Debrock: Newtons Scientific and Philosophical Legacy. Kluwer, Dordrecht 1988, S.47. ISBN 90-247-3723-0
3. ↑ I. Bernard Cohen: Introduction to Newtons Principia. London 1971, S. 53, 296.

Siehe auch

• Zentrifugalkraft
• Gleichförmige Bewegung

Literatur

• Isaac Newton: Philosophiae Naturalis Principia Mathematica. Cambridge, London 1726, neu hrsg. v. Alexandre Koyré, I. Bernard Cohen. London 1971.