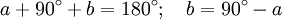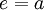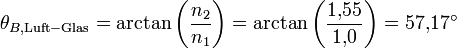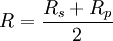- Brewstersches Gesetz
-
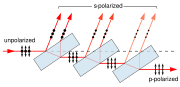
Der Brewster-Winkel (nach Sir David Brewster, 1781–1868) oder Polarisationswinkel ist eine Größe der Optik. Er gibt den Winkel an, bei dem von einfallendem, unpolarisiertem Licht nur die senkrecht zur Einfallsebene (d.h. parallel zur Grenzfläche) polarisierten Anteile reflektiert werden. Das reflektierte Licht ist dann linear polarisiert.
Physikalische Grundlagen
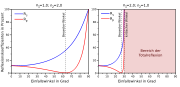
Licht, welches auf eine Grenzfläche zwischen zwei Medien mit den Brechzahlen n1 bzw. n2 trifft, wird gemäß den fresnelschen Formeln reflektiert bzw. transmittiert. Nach den fresnelschen Formeln hängt das Reflexionsvermögen sowohl vom Einfallswinkel Θi = e und von den Brechzahlen n1, n2 als auch von der Polarisation des einfallenden Lichts ab (siehe Abbildung).
Für Licht mit einer Polarisation parallel zur Einfallsebene, welches mit dem Brewster-Winkel einfällt, entfällt die Reflexion. Das Licht dringt vollständig durch die Oberfläche. Licht mit senkrechter Polarisation hingegen wird auch teilweise reflektiert. Das reflektierte Licht ist somit vollständig linear polarisiert.
Im Folgenden wird angenommen, dass der Strahl von der Luft aus auf dieses Material trifft. Für Luft kann man in guter Näherung eine Brechzahl von n1 = 1 annehmen. Das Material habe die Brechzahl n2.
Bei dem Übergang zwischen zwei beliebigen, nicht magnetisierbaren Medien ergibt sich der Brewster-Winkel aus dem snelliusschen Brechungsgesetz:
- n1sinθB = n2cosθB
 (brewstersches Gesetz),
(brewstersches Gesetz),
wobei n1 die Brechzahl des Mediums ist, in dem 'θB gemessen wird, und n2 die Brechzahl des anderen Mediums.
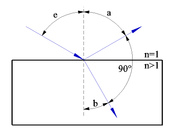
Der eintreffende Lichtstrahl regt die Elektronen des Materials zum Schwingen an (Verschiebungspolarisation). Es entsteht dadurch eine Ansammlung von atomaren Dipolen, die in Polarisationsrichtung schwingen und dadurch Sekundärwellen ausstrahlen. Nach dem optischen Reflexionsgesetz (Einfallswinkel e gleich Reflexionswinkel a) wird der Strahl unter dem Reflexionswinkel reflektiert.
Das Besondere bei Einstrahlung im Brewster-Winkel ist, dass der unter dem Winkel b gebrochene Strahl orthogonal auf dem reflektierten steht. Daher wird das gesamte parallel zur Einfallsebene polarisierte Licht gebrochen und nur der senkrecht zur Einfallsebene polarisierte Anteil reflektiert. Würde auch parallel zur Einfallsebene polarisiertes Licht reflektiert, so ergäbe dies eine longitudinal schwingende Lichtwelle, die aufgrund der Eigenschaften des elektromagnetischen Felds nicht existieren kann (vgl. Strahlungscharakteristik eines Dipols (erzwungene Schwingung): in Richtung der Dipolachse findet keine Abstrahlung statt!).
Beispiel - Reflexion an Glas
Anhand des vorhergehenden Abschnittes ist erkennbar, dass eine Glasplatte als Polarisator verwendet werden kann, indem man sie im Brewster-Winkel bestrahlt.
Mit den oben bezeichneten Winkeln und dem Brechungsgesetz gilt:
Unter der Annahme bei den verwendeten Materialien Luft (n1 = 1) und gewöhnlichem Glas (SiO2, n2 = 1,55) handele es sich um ideale, nicht absorbierende Materialien (Dielektrika), gilt das oben beschriebene brewstersche Gesetz:
Für den Übergang von Luft in Glas ergibt sich ein Brewster-Winkel:
gemäß den Fresnel-Gleichungen ergeben sich für den senkrechten bzw. parallelen Anteil des einfallenden Lichtes folgende Reflexionsgrade (Rs bzw. Rp):
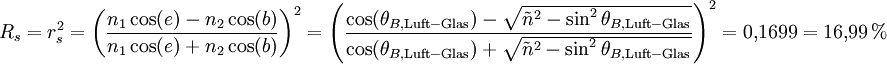
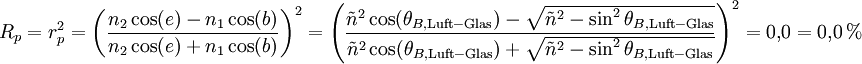
mit
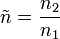 und e = θB,Luft − Glas
und e = θB,Luft − Glasdas reflektierte Licht ist demnach vollständig senkrecht zur Einfallsebene linear polarisiert.
Bei Einstrahlung unpolarisierten Lichts (alle Polarisationen gleich stark vertreten) läßt sich der Reflexionsgrad über das arithmetische Mittel der beiden Komponenten bestimmen, es gilt:
Für den beschriebenen Übergang von unpolarisiertem Licht werden daher nur 8,5 % der eingestrahlten Intensität (im Brewster-Winkel) reflektiert.
Weblinks
Wikimedia Foundation.