Dipol

Erzeugung elektrischer Dipole

(Die rot gefärbte Kugel entspricht der Ladung +Q, die blaue der Ladung -Q)'

Ein Dipol entsteht typischerweise durch Grenzwertbildung aus einer physikalischen Anordnung zweier nahe beieinander befindlicher gegensätzlich geladener Vektoren (z. B. elektrischer Ladungen mit gerichtetem Abstand $\vec p$), welche ein sog. Dipolfeld erzeugen; und zwar erfolgt die Grenzwertbildung so, dass der Abstandsvektor $\vec p$ der Ladungen gegen Null konvergiert, wobei gleichzeitig die Ladungsstärke $\pm Q$ umgekehrt-proportional zum Abstand gegen $\pm\infty$ divergiert  (sog. „Dipol-Limes“).

• Richtung und Betrag des Dipols sind dann durch den Dipolvektor $\vec p$ gegeben (genauer durch $\vec p_Q:=\lim_{|\vec p|\to 0;\,\,|\vec p|\cdot Q\to \rm{konst.}}\,\{\vec p\cdot (+Q)\},$ 
  wobei die Konstante eine positive Zahl ist.

Ein Dipol kann beispielsweise aus elektrischen Ladungen erzeugt werden, kann aber auch ohne räumlich trennbare Ladungen existieren wie beim magnetischen Dipol (es gibt nur fiktive, keine realen magnetischen Ladungen!). Auch in diesem Fall wird der Dipol durch sein vektorielles Dipolmoment $\vec p_Q$ vollständig charakterisiert (im Folgenden wird auch in diesem Fall anstelle von $\vec p_Q$ einfach die Bezeichnung $\vec p$ benutzt.)

Dipole treten in verschiedenen Bereichen auf wie Elektromagnetismus, Akustik oder Fluiddynamik. Charakteristisch ist immer die Richtungsabhängigkeit und Abnahme des erzeugten Feldes mit 1/r³ bei großen Abständen r. Der Begriff des Dipols ist in seiner Bedeutung nicht identisch mit dem des Zweipols, welcher eine bestimmte Gruppe elektrischer Schaltungen beschreibt.

Vorkommen

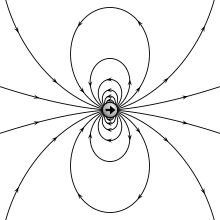
Elektrische Dipole

Elektrische Dipole erfordern die Trennung von Ladungen und treten daher auf makroskopischer Skala nur selten auf. Auf mikroskopischer Skala sind dagegen elektrische Dipole sehr häufig. Beispielsweise werden sie von asymmetrischen Molekülen wie z. B. dem Wassermolekül erzeugt.

Auch in biologischen Muskel- und Nervenfasern entstehen elektrische Dipolmomente durch aufgebaute Spannungen, die beispielsweise beim Elektrokardiogramm gemessen werden können.

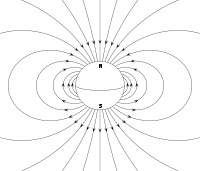
Magnetische Dipole

Magnetisches Dipolfeld der Erde

Wegen des Fehlens magnetischer Monopole sind magnetische Dipole und ihre Überlagerungen die einzigen realen^[1] Quellen magnetischer Felder. Daher sind im Magnetismus auch im makroskopischen Bereich offensichtliche Dipolfelder sehr häufig. So lässt sich auch ein langer Stabmagnet in guter Näherung als ein einziger magnetischer Dipol beschreiben. Auch das Magnetfeld der Erde ähnelt im Außenbereich einem Dipolfeld mit Dipolachse von Nord nach Süd.

Ein magnetischer Dipol entsteht generell aus einer stromumflossenen Fläche oder dem Spin punktförmiger Teilchen.

Oft werden als Dipolmagnet auch größere felderzeugende Konfigurationen bezeichnet, die kein reines Dipolfeld erzeugen sondern ein in erster Näherung konstantes Magnetfeld im Koordinatenursprung, im Gegensatz zu Quadrupolmagneten und höheren Ordnungen.

Hertzscher Dipol

Ein Hertzscher Dipol (bzw. das zugehörige Strahlungsfeld, z. B. das im sog. „Handy“ erzeugte elektromagnetische Feld) entsteht durch die zeitliche Variation eines statischen elektrischen Dipols, beispielsweise wenn eine Dipolantenne von einem Wechselstrom durchlaufen wird. Hierdurch entsteht die einfachste Form eines elektromagnetischen Strahlers. Die Richtcharakteristik des Strahlers erbt dann die Symmetrie um die Dipolachse:

Zeichnerische Darstellung der räumlichen Richtcharakteristik eines Dipols

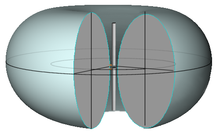
Werden 2D-Richtercharakteristiken vieler Schnittebenen zu einem räumlichen Gebilde zusammengestellt, entsteht eine dreidimensionale Richtcharakteristik. Der Abstand vom Mittelpunkt der Antenne zu jedem Punkt der Oberfläche dieses Körpers gibt die in dieser Richtung bei gleichen Abständen gemessene Intensität an.

Nimmt man an, dass die Intensität senkrecht zum Dipol maximal ist, lässt sich die winkelabhängige Intensität folgendermaßen ausdrücken. Dabei ist α der Winkel zwischen dem Dipol und einer beliebigen Richtung.

I(α) = I₀sin²α

Physikalische Beschreibung

Jeder Dipol ist durch sein Dipolmoment charakterisiert, eine vektorielle Größe, welche Richtung und Betrag besitzt. Dabei steht $\vec p$ für ein elektrisches und im folgenden für ein beliebiges Dipolmoment, wohingegen ein magnetisches Dipolmoment in der Regel mit $\vec m$ bezeichnet wird.

Physikalischer Dipol

Ein physikalischer Dipol ^[2] besteht, wie gesagt, aus zwei gegensätzlichen Ladungen $\pm q$ in hinreichend kurzem Abstand d. Das Dipolmoment ist definiert als

$\vec p = q \cdot \vec d\,.$

Das Feld in großer Entfernung, d.h. für |r| >> d, hängt dann nur noch von $\vec p$ ab und nicht mehr von q und d einzeln. Je größer der Abstand, desto mehr nähert sich das Feld dem eines Punktdipols an. Bei kleinen Abständen weicht das Feld davon ab, was sich auch durch nichtverschwindende höhere Multipolmomente zeigt.

Punktdipol

Feldlinien eines beliebigen Punktdipols

Der Punktdipol entsteht, wenn ein ausgedehnter Dipol ohne Monopolmoment auf einen Punkt verkleinert wird ohne dabei das Dipolmoment zu ändern. Das entspricht dem Grenzfall bei großen Abständen und führt zur Ladungsverteilung

$\rho(\vec r) =-(\vec p \cdot \vec \nabla)\,\delta(\vec r)$

unter Verwendung des Nabla-Operators $\vec \nabla$ und der Delta-Funktion $\delta(\vec r)$.

Der Punktdipol erzeugt das Feldpotential

$\phi(\vec{r}) = \frac {1}{4 \pi \varepsilon_0} \frac {\vec{p} \cdot \vec{r}}{r^3} = \frac {1}{4 \pi \varepsilon_0} \frac {p \cos (\theta)}{r^2}$

und das Vektorfeld

$\vec{E}(\vec{r}) = \frac {1}{4 \pi \varepsilon_0} \left(3\,\frac{\vec{p}\cdot\vec{r}}{r^5}\,\vec{r} - \frac{1}{r^3}\,\vec{p}\right) = \frac {1}{4 \pi \varepsilon_0} \frac{p}{r^3} \left(2\cos(\theta)\cdot\hat{r} + \sin(\theta)\cdot\hat{\theta}\right)$

unter Verwendung des Polarwinkels θ und der Einheitsvektoren $\hat{v}$.

Dipol in der Multipolentwicklung

Felder, die aus einer räumlich begrenzten Ladungsverteilung entstehen, lassen sich durch die Multipolentwicklung nach verschiedenen Anteilen aufspalten, die bei großen Abständen verschieden schnell abfallen. Bei großen Abständen dominiert dann immer der erste nichtverschwindende Term. Der Dipolterm als zweiter Term in der Entwicklung kommt daher besonders zum tragen wenn der Monopolterm (Gesamtladung) verschwindet. Eine beliebige Ladungsverteilung besitzt dann das Dipolmoment

$\vec{p} = \sum_i q_i \cdot \vec{r}_i$.

Falls der Monopolterm allerdings nicht verschwindet, so lässt sich der Wert des Dipolmoments durch Verschiebung des Koordinatenursprungs verändern und ist somit nicht eindeutig definiert.

Der nächsthöhere Term ist das Quadrupolmoment, dessen Feld mit 1/r⁴ abnimmt.

Dipol im äußeren Feld

Ein Dipol im äußeren Feld $\vec E$, das nicht von ihm selbst erzeugt wird, besitzt die potentielle Energie:

$V = -\vec p \cdot \vec E$

In einem inhomogenen äußeren Feld - E-Feld (elektrisches F.) bzw. B-Feld (magnetisches F.) - wirkt auf einen Dipol die Kraft:

$\vec F = (\vec{p} \cdot \vec \nabla)\,\vec E$  bzw.  $\vec{F} = \vec{\nabla}(\vec{m}\cdot\vec{B})$

Diese beiden Ausdrücke sind über die Graßmann-Identität mathematisch identisch, wenn das Feld rotationsfrei ist.

Manchmal benutzt man deshalb auch eine leicht unterschiedliche, äquivalente Konvention für die Definition des magnetischen Moments, nämlich $\vec m_H:=\mu_0 \vec m\,,$ mit der magnetischen Permeabilität $\mu_0\,.$ Dann schreibt man von vornhererin auch im magnetischen Fall $\vec F=(\vec m_H \cdot\vec\nabla )\, \vec H\,.$ ^[3]

Zeigt ein Dipol nicht in Richtung eines äußeren Feldes, so wirkt auf ihn ein Drehmoment:

$\vec M = \vec p \times \vec E$ bzw.  $\vec M = \vec m_H \times \vec H\,.$

Befinden sich zwei Dipole im Feld des jeweils anderen, so entstehen Dipol-Dipol-Kräfte, die entsprechend dem Feldgradienten mit 1/r⁴ abnehmen.

Einzelnachweise und Fußnoten

1. ↑ D.h. erneut: es gibt nur fiktive magnetische Ladungen
2. ↑ An dieser Stelle wird absichtlich nicht der Großbuchstabe Q, sondern der Kleinbuchstabe q benutzt, um zu betonen, dass hier keine explizite Limesbildung erfolgt.
3. ↑ Dies hat u.a. deshalb Vorteile, weil die im Festköpermagnetismus wichtige Größe der Magnetisierung eines Permanentmagneten dieselbe physikalische Dimension wie $\vec H$ hat (und nicht wie $\vec B )\,.$