Fresnelsche Formeln

Partielle Reflexion und Transmission einer eindimensionalen Welle an einer Potentialstufe. Der Anteil der reflektierten und transmittierten Intensität einer elektromagnetischen Welle lässt sich mit den fresnelschen Formeln berechnen

Die fresnelschen Formeln (nach Augustin Jean Fresnel) beschreiben quantitativ die Reflexion und Transmission einer ebenen, elektromagnetischen Welle an einer ebenen Grenzfläche. Der zunächst berechnete Reflexions- und Transmissionsfaktor ist das Verhältnis der reflektierten bzw. transmittierten Amplitude zu jener der einfallenden Welle. Durch Quadrieren erhält man den Reflexions- bzw. den Transmissionsgrad, welche als Energiegrößen Intensitätsverhältnisse darstellen.

Vorbetrachtungen

Die fresnelschen Formeln können aus den maxwellschen Gleichungen hergeleitet werden, dabei nutzt man Sonderfälle der Randbedingungen elektromagnetischer Wellen an einer ladungs- und stromfreien Grenzschicht:

$\vec{n}\times (\vec{E}_2-\vec{E}_1)=0$	$\vec{n}\times (\vec{H}_2-\vec{H}_1)=0$
$\vec{n}\cdot(\vec{D}_2-\vec{D}_1)=0$	$\vec{n}\cdot (\vec{B}_2-\vec{B}_1)=0$

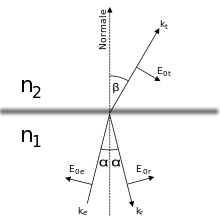
Hierbei ist $\vec{n}$ die Normale auf die Grenzfläche und die anderen Größen beschreiben Magnetfeld und elektrisches Feld in den beiden Medien. Die Tangentialkomponente der elektrischen Feldstärke E und der magnetischen Feldstärke H sind an der Grenzfläche stetig, ebenso wie die Normalkomponente der elektrischen Flussdichte D und der magnetischen Flussdichte B (tangential und normal bezieht sich auf die Grenzfläche).

Abhängig von der Polarisation der einfallenden Welle ergeben sich unterschiedliche Randbedingungen für das Auftreffen einer elektromagnetischen Welle auf eine optische Grenzfläche. Jede beliebig polarisierte elektromagnetische Welle lässt sich als Superposition zweier linear polarisierter Wellen, die senkrecht zueinander schwingen, darstellen. Als Bezugsebene dient die Einfallsebene, die vom Wellenvektor $\vec{k_e}$ der einfallenden Welle und der Flächennormalen $\vec{n}$ aufgespannt wird. Eine einfallende, beliebig polarisierte Welle lässt sich also als Superposition einer parallel (p) und senkrecht (s) zur Einfallsebene polarisierten Welle schreiben:

$\vec{E}=\left[ (E_{0e})_{s}\ \vec{e}_{s}\ e^{i\delta _{s}}+(E_{0e})_{p}\ \vec{e}_{p}\ e^{i\delta _{p}} \right]\ e^{i(\vec{k}_{e}\cdot \vec{r}-\omega t)}=(E_{0e})_{s}\ \vec{e}_{s}\ e^{i(\vec{k}_{e}\cdot \vec{r}-\omega t+\delta _{s})}+(E_{0e})_{p}\ \vec{e}_{p}\ e^{i(\vec{k}_{e}\cdot \vec{r}-\omega t+\delta _{p})}$

Dabei ist $\vec{E}$ der Feldvektor des elektrischen Feldes, $\vec{e}_i$ sind die Einheitsvektoren für s- und p-Polarisation, und die Parameter δ_i entsprechen beliebigen Phasenverschiebungen.

Wegen des Superpositionsprinzips reicht es aus, die Amplitudenverhältnisse für parallel und senkrecht zur Einfallsebene linear polarisierte Wellen zu berechnen.

Die Polarisationsrichtung (senkrecht bzw. parallel zur Einfallsebene) bleibt nach der Reflexion unverändert.

Allgemeiner Fall

Einfluss der komplexen Brechzahl eines Materials (n₁ + ik₁) auf das Reflexionsverhalten eines Lichtstrahls beim Auftreffen auf die Grenzfläche Luft/Material

Im allgemeinen Fall haben beide Medien eine unterschiedliche Permittivität $\varepsilon_r$ und Permeabilität μ_r sowie eine komplexe Brechzahl

$N = n +\mathrm i k\,$.

Vorbetrachtung für Gleichungen mit eliminiertem Brechungswinkel

Im Allgemeinen sind für die Berechnung der Reflexions- bzw. Transmissionsgrade mit den fresnelschen Formeln sowohl beide Brechzahlen der beteiligten Medien als auch der Einfalls- und Brechungswinkel notwendig.

Um neben diesen allgemeinen Gleichungen auch eine vom Brechungswinkel unabhängige Form anzugeben, muss der Brechungswinkel aus der allgemeinen Form eliminiert werden. Da beide Winkel (α und β) über das snelliussche Brechungsgesetz verknüpft sind, kann dies wie folgt (mit Hilfe einer Falleingrenzung) erreicht werden:

$N_{1}\sin \alpha =N_{2}\sin \beta\,$ (Brechungsgesetz)

quadrieren liefert (unter Nutzung einer trigonometrischen Umrechnung) folgenden Zusammenhang:

$N_{1}^{2}\sin ^{2}\alpha =N_{2}^{2}\sin ^{2}\beta =N_{2}^{2}\left( 1-\cos ^{2}\beta \right)$

Umgestellt ergibt sich daraus:

$\cos \beta =\pm \frac{\sqrt{N_{2}^{2}-N_{1}^{2}\sin ^{2}\alpha }}{N_{2}}$

Als Lösung wird der Fall mit dem positiven Vorzeichen genutzt, damit später der Reflexionsfaktor r ≤ 1 ist.

Senkrechte Polarisation (TE)

Bei der senkrechten Polarisation bildet die elektrische Komponente mit der Einfallsebene einen rechten Winkel

Als erstes betrachtet man die Komponente, die linear senkrecht (Index: s) zur Einfallsebene polarisiert ist. Sie wird in der Literatur auch häufig als transversalelektrische (TE) Komponente bezeichnet.

$\left( \frac{E_{0t}}{E_{0e}} \right)_{s}=t_{s}=\frac{2 N _{1}\cos \alpha }{N_{1}\cos \alpha +\frac{\mu _{r1}}{\mu _{r2}}N_{2}\cos \beta }=\frac{2N_{1}\cos \alpha }{N_{1}\cos \alpha +\frac{\mu _{r1}}{\mu _{r2}}\sqrt{N_{2}^{2}-N_{1}^{2}\sin ^{2}\alpha }}$

$\left( \frac{E_{0r}}{E_{0e}} \right)_{s}=r_{s}=\frac{N_{1}\cos \alpha -\frac{\mu _{r1}}{\mu _{r2}}N_{2}\cos \beta }{N_{1}\cos \alpha +\frac{\mu _{r1}}{\mu _{r2}}N_{2}\cos \beta }=\frac{N_{1}\cos \alpha -\frac{\mu _{r1}}{\mu _{r2}}\sqrt{N_{2}^{2}-N_{1}^{2}\sin ^{2}\alpha }}{N_{1}\cos \alpha +\frac{\mu _{r1}}{\mu _{r2}}\sqrt{N_{2}^{2}-N_{1}^{2}\sin ^{2}\alpha }}$

Mit dem Transmissionsfaktor t_s und Reflexionsfaktor r_s.

Parallele Polarisation (TM)

Bei paralleler Polarisation schwingt die elektrische Komponente in der Einfallsebene

Reflexion parallel polarisiert

Im anderen Fall wird die Amplitude einer in der Einfallsebene linear parallel (Index: p) polarisierten Welle betrachtet. Sie wird in der Literatur auch häufig als transversalmagnetische (TM) Komponente bezeichnet.

$\left( \frac{E_{0t}}{E_{0e}} \right)_{p}=t_{p}=\frac{2N_{1}\cos \alpha }{N_{2}\frac{\mu _{r1}}{\mu _{r2}}\cos \alpha +N_{1}\cos \beta }=\frac{2N_{1}N_{2}\cos \alpha }{N_{2}^{2}\frac{\mu _{r1}}{\mu _{r2}}\cos \alpha +N_{1}\sqrt{N_{2}^{2}-N_{1}^{2}\sin ^{2}\alpha }}$

$\left( \frac{E_{0r}}{E_{0e}} \right)_{p}=r_{p}=\frac{N_{2}\frac{\mu _{r1}}{\mu _{r2}}\cos \alpha -N_{1}\cos \beta }{N_{2}\frac{\mu _{r1}}{\mu _{r2}}\cos \alpha +N_{1}\cos \beta }=\frac{N_{2}^{2}\frac{\mu _{r1}}{\mu _{r2}}\cos \alpha -N_{1}\sqrt{N_{2}^{2}-N_{1}^{2}\sin ^{2}\alpha }}{N_{2}^{2}\frac{\mu _{r1}}{\mu _{r2}}\cos \alpha +N_{1}\sqrt{N_{2}^{2}-N_{1}^{2}\sin ^{2}\alpha }}$

Die Richtungen der elektrischen Feldvektoren $\vec E_r$ bzw. $\vec E_t$ entsprechen den Richtungen der Vektoren $\vec n_e \times \vec k_r$ bzw. $\vec n_e \times \vec k_t$, wobei $\vec n_e$ der Normalenvektor der Einfallsebene ist.

Spezialfall: gleiche magnetische Permeabilität

Für den in der Praxis häufigen Spezialfall, dass die beteiligten Materialien näherungsweise die gleiche magnetische Permeabilität besitzen (μ_r1 = μ_r2), z. B. μ_r = 1 für nicht magnetische Materialien, vereinfachen sich die Fresnel-Formeln wie folgt:

Senkrechte Polarisation (TE)

$\left( \frac{E_{0t}}{E_{0e}} \right)_s = t_s = \frac{2 N_1 \cos{\alpha}}{ N_1\cos{\alpha}+ N_2\cos{\beta}}$

$\left( \frac{E_{0r}}{E_{0e}} \right)_s = r_s =\frac{ N_1\cos{\alpha}- N_2\cos{\beta}}{ N_1\cos{\alpha}+ N_2\cos{\beta}}$

Parallele Polarisation (TM)

$\left( \frac{E_{0t}}{E_{0e}} \right)_p = t_p =\frac{2 N_1 \cos{\alpha}}{ N_2\cos{\alpha}+ N_1\cos{\beta}}$

$\left( \frac{E_{0r}}{E_{0e}} \right)_p = r_p =\frac{ N_2\cos{\alpha}- N_1\cos{\beta}}{ N_2\cos{\alpha}+ N_1\cos{\beta}}$

Spezialfall: dielektrische Materialien

Amplitudenverhältnisse r,t (oben) und Reflexions-/ Transmissionsvermögen R,T (unten) für die Grenzfläche Luft n = 1 und Glas n = 1,5 (μ₁ = μ₂ = 1 und κ₁ = κ₂ = 0). Auf Grenzfläche einfallendes Licht von der Luftseite (links) und von der Glasseite (rechts).

Ein weiterer Spezialfall ergibt sich für ideale Dielektrika, bei denen der Absorptionskoeffizient κ der komplexen Brechzahl gleich null ist, d. h., das Material (auf beiden Seiten der Grenzfläche) absorbiert die entsprechende elektromagnetische Strahlung nicht (k₁ = k₂ = 0). Es gilt:

$N_i = n_i( 1+\mathrm i \kappa_i) = n_i+\mathrm i k _i\quad\xrightarrow[]{k_i = 0} \quad N_i = n_i$

Durch den Wegfall der komplexen Anteile vereinfachen sich die fresnelschen Formeln wie folgt:

Senkrechte Polarisation (TE)

$\left( \frac{E_{0t}}{E_{0e}} \right)_s = t_s =\frac{2n_1 \cos{\alpha}}{n_1\cos{\alpha}+n_2\cos{\beta}}=\frac{2 \sin{\beta}\cos{\alpha}}{\sin{(\alpha+\beta)}}$

$\left( \frac{E_{0r}}{E_{0e}} \right)_s = r_s =\frac{n_1\cos{\alpha}-n_2\cos{\beta}}{n_1\cos{\alpha}+n_2\cos{\beta}}=-\frac{\sin{(\alpha-\beta)}}{\sin{(\alpha+\beta)}}$

Parallele Polarisation (TM)

$\left( \frac{E_{0t}}{E_{0e}} \right)_p = t_p =\frac{2n_1 \cos{\alpha}}{n_2\cos{\alpha}+n_1\cos{\beta}}=\frac{2\sin{\beta}\cos{\alpha}}{\sin{(\alpha+\beta)}\cos{(\alpha-\beta)}}$

$\left( \frac{E_{0r}}{E_{0e}} \right)_p = r_p =\frac{n_2\cos{\alpha}-n_1\cos{\beta}}{n_2\cos{\alpha}+n_1\cos{\beta}}=\frac{\tan{(\alpha-\beta)}}{\tan{(\alpha+\beta)}}$

Hinweis: Das zweite Gleichheitszeichen ergibt sich durch Anwenden des Brechungsgesetzes $\frac{n_{1}}{n_{2}}=\frac{\sin \beta }{\sin \alpha }$ und Additionstheoremen.^[1] Die dabei getroffenen Annahmen sind für Einfallswinkel von 0° und 90° nicht gültig und die Formeln können daher nicht genutzt werden. Hierfür muss die ursprüngliche Form aus reinen Kosinus-Termen verwendet werden

Senkrechter Einfall

Eine weitere Vereinfachung ergibt sich für den Fall, dass der Einfallswinkel α gleich dem Brechungswinkel β ist (senkrechter Einfall):

$\left(\frac{E_{0r}}{E_{0e}} \right)_s = r_s =\frac{n_1-n_2}{n_1+n_2} = - r_p = -\left(\frac{E_{0r}}{E_{0e}} \right)_p$

Fällt beispielsweise sichtbares Licht senkrecht auf die Grenzfläche Luft-Quarzglas, wird der Anteil

$\left( \frac{E_\mathrm{0r}}{E_\mathrm{0e}} \right)^2 = r^2 = R = \left( \frac{1{,}46-1}{1{,}46+1} \right)^2 = 0{,}035 = 3{,}5\,%$

der einfallenden Intensität unabhängig von der Polarisation reflektiert (vgl. Abschnitt Zusammenhang mit Reflexions- und Transmissionskoeffizienten).

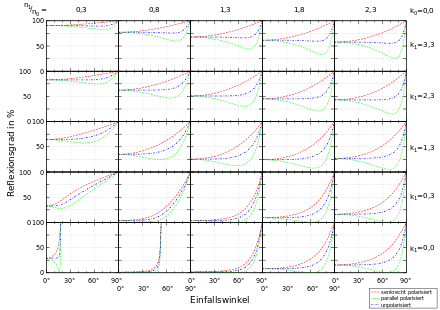
Diskussion der Amplitudenverhältnisse

Dort, wo die Amplitudenkoeffizienten reell und negativ sind, tritt ein Phasensprung von $180^\circ=\pi$ auf (bei reell und positiv keine Phasenänderung):

$r= -| r |=|r| \cdot e^{i\pi }$

Das Amplitudenverhältnis r_p besitzt einen Nulldurchgang am Brewster-Winkel α_B:

$r_{p}=\frac{\tan (\alpha -\beta )}{\tan (\alpha +\beta )}=0$   genau bei   $\alpha +\beta =90{}^\circ$

$\frac{n_{2}}{n_{1}}=\frac{\sin \alpha }{\sin \beta }=\frac{\sin \alpha }{\sin (90{}^\circ -\alpha )}=\frac{\sin \alpha }{\cos \alpha }=\tan \alpha$   also   $\alpha _{\text{B}}=\arctan \frac{n_{2}}{n_{1}}$

Beispiele: Brewster-Winkel für Luft-Glas $\tfrac{n_{2}}{n_{1}}=\tfrac{1{,}5}{1}$ ist $\alpha _{\text{B}}=56{,}3{}^\circ$ und für Glas-Luft $\tfrac{n_{2}}{n_{1}}=\tfrac{1}{1{,}5}$ ist $\alpha _{\text{B}}=33{,}7{}^\circ$.

Für n₂ < n₁ werden ab einem bestimmten Winkel die Amplitudenverhältnisse komplex. Ab diesem kritischen Winkel oder Grenzwinkel tritt Totalreflexion auf. Der Grenzwinkel α_c entspricht dem Brechungswinkel $\beta =90{}^\circ$ also sinβ = 1, d. h., die Welle läuft an der Grenzfläche entlang.

$\frac{n_{2}}{n_{1}}=\frac{\sin \alpha }{\sin 90{}^\circ }=\sin \alpha$   also   $\alpha _{\text{c}}=\arcsin \frac{n_{2}}{n_{1}}$

Beispiel: Grenzwinkel für Glas-Luft $\tfrac{n_{2}}{n_{1}}=\tfrac{1}{1{,}5}$ ist $\alpha _{\text{c}}=41{,}8{}^\circ$.

Zusammenhang mit Reflexions- und Transmissionskoeffizienten

Reflexionskoeffizient in Abhängigkeit des Einfallswinkels beim Einfall von Licht auf die Grenzfläche zweier idealer Dielektrika (k₁ = k₂ = 0)

Man betrachte ein Strahlenbündel, das auf der Grenzfläche die Fläche A bestrahlt. Somit sind die Strahlquerschnitte des einfallenden, reflektierten bzw. transmittierten Strahls gleich Acosα, Acosα bzw. Acosβ. Die Energie, die pro Zeit- und Flächeneinheit durch eine Fläche, deren Normale parallel zur Energieflussrichtung $\vec S$ (bei isotropen Medien gleich Ausbreitungsrichutung $\vec k$) steht, fließt, ist gegeben durch den Poynting-Vektor $\vec S$:

$\vec{S} = \frac{1}{\mu_0} \,(\vec{E} \times \vec{B})$

$S=\varepsilon _{0}cN E^{2}$

Die mittlere Energieflussdichte erhält man durch zeitliche Mittelung:

$I=\left\langle S \right\rangle=\frac{\varepsilon _{0}cN}{2}\left| E_{0}\right| ^{2}$

Die mittlere Energie, die pro Zeiteinheit vom Strahlenbündel transportiert wird (mittlere Leistung, die auf Fläche A trifft), entspricht der mittleren Energieflussdichte mal der Querschnittsfläche, also

$I_e A\,\cos \alpha$,

$I_r A\,\cos \alpha$

bzw.

$I_t A\,\cos \beta$.

Allgemein (unpolarisiertes Licht) wird der Reflexionskoeffizient R (oft auch mit ρ bezeichnet) folgendermaßen definiert:

$R=\frac{\text{reflektierte Leistung}}{\text{eingestrahlte Leistung}}=\left| \frac{A\left\langle \vec{S}_{r} \right\rangle \cdot \vec{n}}{A\left\langle \vec{S}_{e} \right\rangle \cdot \vec{n}} \right|=\left| \frac{I_{r}A\cos \alpha }{I_{e}A\cos \alpha } \right|=\left| \frac{N_{1}\cos \alpha }{N_{1}\cos \alpha } \right|\left| \frac{E_{0r}}{E_{0e}} \right|^{2}=\left| \frac{E_{0r}}{E_{0e}} \right|^{2}$

und als Transmissionskoeffizienten T (oft auch mit τ bezeichnet):

$T=\frac{\text{transmittierte Leistung}}{\text{eingestrahlte Leistung}}=\left| \frac{A\left\langle \vec{S}_{t} \right\rangle \cdot \vec{n}}{A\left\langle \vec{S}_{e} \right\rangle \cdot \vec{n}} \right|=\left| \frac{I_{t}A\cos \beta }{I_{e}A\cos \alpha } \right|=\left| \frac{N_{2}\cos \beta }{N_{1}\cos \alpha } \right|\left| \frac{E_{0t}}{E_{0e}} \right|^{2}$

Die beiden Koeffizienten lassen sich nun mit Hilfe der Fresnelschen Formeln berechnen, sie sind das Produkt des entsprechenden Reflexions- bzw. Transmissionsfaktors mit dessen konjugiert komplexem Wert.

$R_{i}=\left| \left( \frac{E_{0r}}{E_{0e}} \right)_{i} \right|^{2}=r_{i}\cdot \bar{r}_{i}$

$T_{i}=\left| \frac{N_{2}\cos \beta }{N_{1}\cos \alpha } \right|\left| \left( \frac{E_{0t}}{E_{0e}} \right)_{i} \right|^{2}=\left| \frac{N_{2}\cos \beta }{N_{1}\cos \alpha } \right|t_{i}\cdot \bar{t}_{i}$

Für ideale Dielektrika, die keinen Absorptionskoeffizienten aufweisen und deren Reflexionsfaktoren reell sind, vereinfachen sich die Gleichungen zu:

$R_{i}=\left| \left( \frac{E_{0r}}{E_{0e}} \right)_{i} \right|^{2}=r_{i}^{2}$

$T_{i}=\frac{n_{2}}{n_{1}}\frac{\cos \beta }{\cos \alpha }\left| \left( \frac{E_{0t}}{E_{0e}} \right)_{i} \right|^{2}=\frac{n_{2}}{n_{1}}\frac{\cos \beta }{\cos \alpha }t_{i}^{2}=\frac{\tan \alpha }{\tan \beta }t_{i}^{2}$

mit i für die s- bzw. p-polarisierte Komponente.

Ohne Absorption gilt folgende Energiestrombilanz für die einzelnen Polarisationsrichtungen:

T_s + R_s = 1

T_p + R_p = 1

Mit der Gesamtamplitude $\left| E_{0i} \right|^{2}=\left| E_{0i} \right|_{p}^{2}+\left| E_{0i} \right|_{s}^{2}$ (i für die einfallende, reflektierte oder transmittierte Welle) gilt ohne Absorption die Gesamtenergiestrombilanz:

T + R = 1

Literatur

• Wolfgang Nolting: Grundkurs Theoretische Physik 3: Elektrodynamik. 7. Auflage. Springer, Berlin 2002, ISBN 3-540-20509-8
• Wolfgang Demtröder: Experimentalphysik 2. Springer, Berlin 2004, ISBN 3-540-20210-2.
• John David Jackson: Klassische Elektrodynamik. de Gruyter, Berlin 2006, ISBN 3-11-018970-4.
• Karl J. Ebeling : Integrierte Optoelektronik: Wellenleiteroptik, Photonik, Halbleiter. 2. Auflage, Springer. Berlin 1998, ISBN 3-540-54655-3.

Weblinks

 Commons: Fresnelsche Formeln – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

1. ↑ Eugene Hecht: Schaum's outline of theory and problems of optics. McGraw-Hill Professional, 1975, ISBN 0070277303, S. 40–50.