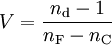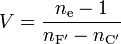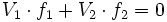Abbe-Zahl

Die abbesche Zahl (oder Abbe-Zahl) gibt in der Optik die optische Dispersion eines transparenten Mediums im Verhältnis zur Brechzahl an. Die abbesche Zahl ist nach dem deutschen Physiker Ernst Abbe (1840–1905) benannt. Sie ist eine dimensionslose Größe und besitzt somit keine Einheit.

Grundlagen

Optische Dispersion bedeutet, dass die Brechung des Lichts von der Wellenlänge (und somit von der Farbe) abhängig ist, dadurch entsteht bei Linsenoptiken die chromatische Aberration, ein Abbildungsfehler, der z. B. zu farbigen Rändern rund um Bilder heller Objekte führt.

Für eine vollständige Beschreibung der Dispersion eines Materials (z. B. einer Glassorte) müsste man angeben, wie sich die Brechzahl n des Materials unter Variation der Wellenlänge λ des Lichts ändert, also die komplette Funktion n(λ). Für einfache Berechnungen ist es jedoch oft ausreichend, die Dispersion im Bereich des sichtbaren Lichts durch nur eine Zahl zu beschreiben.

Definition

Wellenlänge λ in nm	Fraunhofer-Linie	Lichtquelle	Farbe
365,0146	i	Hg	UV
404,6561	h	Hg	violett
435,8343	g	Hg	blau
479,9914	F'	Cd	blau
486,1327	F	H	blau
546,0740	e	Hg	grün
587,5618	d	He	gelb
589,2938	D	Na	gelb
643,8469	C'	Cd	rot
656,2725	C	H	rot
706,5188	r	He	rot
768,2	A'	K	rot
852,11	s	Cs	IR
1013,98	t	Hg	IR

Die abbesche Zahl V ist als

$V = \frac{n_{\rm d} - 1}{n_{\rm F} - n_{\rm C}}$

oder neu:

$V = \frac{n_{\rm e} - 1}{n_{\rm F'} - n_{\rm C'}}$

definiert, wobei n_d (bzw. n_e), n_F' und n_C' die Brechzahlen des Materials bei den Wellenlängen der

[ALT] d-, F'- und C'-Fraunhoferlinien (587,6 nm, 486,1 nm und 656,3 nm) bzw.

[NEU] e-, F'- und C'-Fraunhoferlinien (546,07 nm, 479,99 nm und 643,84 nm) sind,

wie in der untenstehenden Tabelle aufgeführt.

Ein Material mit geringer Dispersion hat eine hohe abbesche Zahl. Der reziproke Wert der abbeschen Zahl wird auch oft als relative Dispersion bezeichnet.

Typische Zahlenwerte reichen bei den am häufigsten verwendeten Glassorten von 20 („schweres“, also Blei-reiches Flintglas) bis 60 (Kronglas). Spezielle Glassorten (Fluorit-Kronglas) haben abbesche Zahlen um 85; Magnesiumfluorid sogar eine abbesche Zahl von 95, zeichnet sich also durch besonders geringe Dispersion aus.

Die folgende Tabelle führt Standard-Wellenlängen auf, bei denen die Brechzahl gewöhnlich bestimmt wird, was durch tiefgestellte Buchstaben angezeigt ist.^[1] Zum Beispiel wird n_D bei einer Wellenlänge von 589,3 nm gemessen:

Anwendungen

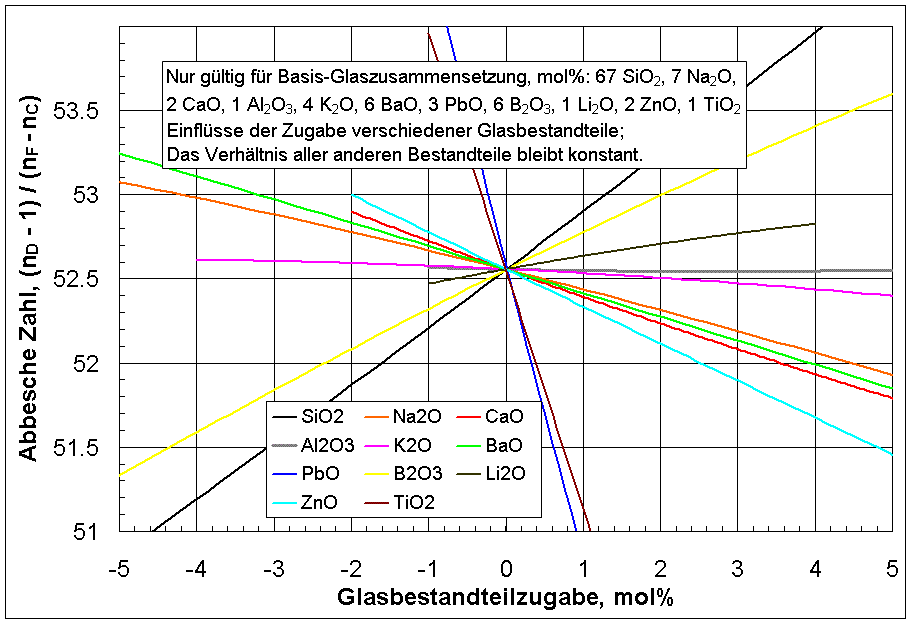Einflüsse der Zugabe ausgewählter Glasbestandteile auf die Abbesche Zahl eines speziellen Basisglases. (^[2]).

Die abbesche Zahl ist vor allem für den Entwurf einfacher Linsensysteme, bei denen die chromatische Aberration minimiert werden soll, von Bedeutung. So hat beispielsweise ein aus zwei dünnen benachbarten Linsen bestehendes System für die Fraunhoferschen Linien F und C die gleiche Brennweite, wenn

$V_1 \cdot f_1 + V_2 \cdot f_2 = 0$

ist, wobei V_i die Abbeschen Zahlen und f_i die Brennweiten der Linsen sind. Da ein solches Linsensystem also blaues und rotes Licht (zumindest bei jeweils zwei „zueinander passenden“ Wellenlängen) gleich abbildet, ist die chromatische Aberration nur mehr relativ gering (man sieht meistens einen violetten Saum um helle Objekte). Solche Linsensysteme sind als Achromaten bekannt und waren die Grundlage für den Bau großer Linsenfernrohre im 19. Jahrhundert.

Für genaue Rechnungen und qualitativ hochwertige Optiken muss die exakte Dispersionsrelation, also die genaue Abhängigkeit der Brechzahl von der Wellenlänge verwendet werden. Trotzdem hilft auch hier die abbesche Zahl, um Glassorten grob zu klassifizieren.

Im Bereich von Infrarot und Ultraviolett ist die abbesche Zahl, die ja für Wellenlängen im Bereich des sichtbaren Lichts definiert ist, ungeeignet.

Einzelnachweise

1. ↑ L. D. Pye, V. D. Fréchette, N. J. Kreidl: Borate glasses: structure, properties, applications. Plenum Press, New York, 1978, ISBN 9780306400162. 
2. ↑ Glassproperties.com Calculation of Abbe's Number for Glasses