Linse (Optik)

Als Linse bezeichnet man ein optisch wirksames Bauelement mit zwei lichtbrechenden Flächen, von denen mindestens eine Fläche konvex oder konkav gewölbt ist. Die wichtigste Eigenschaft einer Linse oder eines Linsensystems ist die optische Abbildung.

Linse (bikonvex)

Aufbau

Die wesentlichste Größe einer Linse ist die Brennweite (Einheit: Meter), d. h. der Abstand von Brennpunkt bzw. Brennebene zur Linse. Der Kehrwert der Brennweite wird als Brechwert (Einheit: Dioptrien) angegeben.

Der Durchmesser der nutzbaren Fläche (Öffnung) einer Linse wird Apertur genannt. Mit den Linsenparametern Apertur, Linsenradien, Mittendicke, Passfehlertoleranz (resp. Wellenfrontfehler im Durchtritt), Sauberkeit, Antireflexionsschicht-System und den Materialkenngrößen Homogenität, Spannungsdoppelbrechung, Brechungsindex und Abbesche Zahl ist die optische Wirkung einer Linse vollständig vorhersagbar.

Als Linsenmaterial sind für sichtbares Licht transparente Stoffe, wie Glas, Kristalle und einige Kunststoffe (z. B. Polycarbonate, Polymethylmethacrylat, Cyclo-Olefin-(Co)polymere) geeignet. Glaslinsen werden durch Vor- und Feinschleifen, Vor- und Feinpolieren (auf Synchrospeed, Pech, CCP, des Weiteren durch magnetorheologisches Polieren und Ion-Beam Figuring) und Zentrieren, bei geringeren Qualitätsanforderungen auch durch Pressen bei hohen Temperaturen gefertigt. Kunststofflinsen werden durch Spritzgießen oder Spritzprägen hergestellt.

Geschichte

Die ersten Linsen wurden für die Korrektur von Kurz- und Weitsichtigkeit als Brillengläser verwendet. Einige Zeit später wurden die ersten Fernrohre und Mikroskope als optische Apparate aus Linsen aufgebaut. Auch die Kontaktlinse gehört zu den hier beschriebenen Linsen.

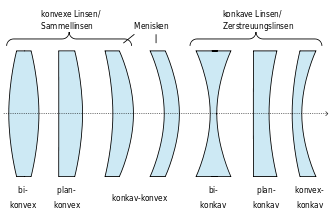
Verschiedene Linsenformen

Bezeichnung von Linsen nach Krümmung ihrer Flächen

Sphärische Linsen

Bei den einfachsten Linsen sind die beiden optisch aktiven Flächen sphärisch. Das heißt, sie sind Oberflächenausschnitte einer Kugel. Daher kann man diesen Flächen (vorzeichenbehaftete) Krümmungsradien zuordnen, die konventionell (DIN 10110) in Lichtrichtung mit R₁, R₂ usw. bezeichnet werden und negativ sind, falls der Krümmungsmittelpunkt auf der Einfallsseite liegt.

Jede dieser Flächen kann konvex, plan (eben) oder konkav sein:

• Konvexe Fläche: Die Fläche ist nach außen gewölbt, R₁, −R₂ > 0.
• Plane Fläche: Die Krümmung ist null, R = ±∞.
• Konkave Fläche: Die Fläche ist nach innen gewölbt, R₁, −R₂ < 0.

Die durch die Krümmungsmittelpunkte verlaufende Gerade wird als optische Achse O bezeichnet, siehe nebenstehende Abbildungen. Ist eine der beiden Linsenflächen plan, so steht die optische Achse senkrecht auf dieser Planfläche. Konventionell kommt das Licht von links (oder von oben).

Darstellung einer Sammellinse, R₂ < 0

Darstellung einer Zerstreuungslinse R₁ < 0, f < 0

Man unterscheidet:

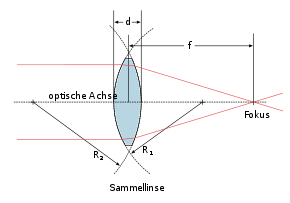
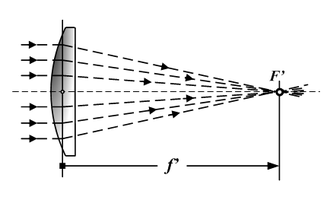
• Sammellinsen mit zwei konvexen Flächen oder mit einer konvexen und einer ebenen Fläche, jedenfalls in der Mitte, im Bereich der optischen Achse, dicker als am Rand; ein Bündel parallel zur optischen Achse einfallender Lichtstrahlen wird idealerweise in einem Punkt hinter der Linse, dem Brennpunkt oder Fokus F, gesammelt. Ihre Brennweite f ist positiv.
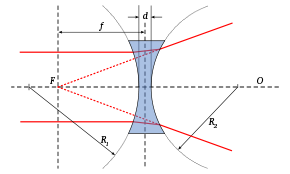
• Zerstreuungslinsen mit zwei konkaven Flächen oder mit einer konkaven und einer ebenen Fläche, jedenfalls am Rand dicker als in der Mitte; ein Bündel von einfallenden Parallelstrahlen läuft hinter der Linse so auseinander, als käme es von einem Punkt auf der Einfallseite des Lichts. Die Brennweite ist negativ.

Daneben gibt es Linsen, die eine konkave und eine konvexe Fläche besitzen; solche Linsen dienen oft zur Korrektur von Abbildungsfehlern (s. u.) in optischen Systemen mit mehreren Linsen. Sie sind Sammellinsen, falls die konvexe Fläche stärker gekrümmt ist, oder Zerstreuungslinsen, falls die konkave Fläche stärker gekrümmt ist.

Ein Bauelement mit zwei planen und parallelen optisch wirksamen Flächen heißt Planplatte oder planparallele Platte.

Sphärische Linsen führen prinzipbedingt zu Abbildungsfehlern, weil der Brennpunkt der Randstrahlen nicht mit dem Brennpunkt weiter innen liegender Strahlen übereinstimmt, gegebenenfalls auch abhängig von der Wellenlänge des Lichts. Um diese Fehler zu verringern, werden Linsensysteme (Anastigmate, Cooke-Triplet, Tessar u. a.) verwendet, die die Fehler weitgehend kompensieren.

Asphärische Linsen

→ Hauptartikel: Asphärische Linse

Asphärische Linsen eignen sich, um Abbildungsfehler durch sphärische Optik zu vermindern. Sie sind rotationssymmetrisch, jedoch sind die Flächen nicht Ausschnitte von Kugeloberflächen. Die so entstandenen Freiheitsgrade im Vergleich zur sphärischen Linse können genutzt werden, um beispielsweise Abbildungsfehler zu reduzieren. Konventionell werden in optischen Systemen Abbildungsfehler durch den Einsatz mehrerer sphärischer Linsen aus unterschiedlichen Materialien (Brechungsindex, Dispersion) korrigiert. Durch den Einsatz einer asphärischen Fläche kann der Optikdesigner im Allgemeinen 2 bis 3 sphärische Linsen ersetzen. Nachteil asphärischer Linsen sind ihre vergleichsweise hohen Herstellungskosten.

Eine Alternative für asphärische Linsen sind Gradientenlinsen.

Ideale Linse

• Möchte man parallel zur optischen Achse einfallendes Licht exakt in einem Punkt bündeln, so lässt sich dies z. B. durch die Wahl einer Linsenform erreichen, bei der die dem einfallenden Licht zugewandte Seite der Linse plan ist und die abgewandte Seite der Linse die Form eines Hyperboloids hat. Für den halben Öffnungswinkel α des zum Hyperboloid gehörenden Asymptotenkegels muss $n\cdot\cos\alpha=1$ gelten, mit dem Brechungsindex n des Linsenmaterials. Die einfallenden Strahlen werden gerade in einem der beiden Hyperbelbrennpunkte gebündelt – in jenem mit dem größeren Abstand zum Scheitel der Linse.
• Für Licht, das nicht parallel einfällt, sondern von einem Punkt auf der optischen Achse entspringt, ist die plane Fläche der Linse durch eine Sphäre um diesen Punkt zu ersetzen und die hyperbolische Fläche durch ein kartesisches Oval. Diese Form ist so konstruiert, dass der optische Weg zwischen beiden Punkten für alle Strahlen des Bündels konstant ist, was nach dem Fermatschen Prinzip die Abbildung bewirkt.

Für den Fall, dass benachbarte Punkte des Urbildes gleichmäßig auf benachbarte Punkte des Bildes abgebildet werden sollen, sind solche Überlegungen noch wesentlich komplexer.

Zylinderlinsen

Unsichtbarkeits-Paradoxon mit Zylinder-Linsen-Hälften: das Bild oben sieht ein Betrachter, der durch die halbe Zylinderlinse unten rechts auf die roten Tiere blickt; diese sind jedoch nicht zu sehen, da die Strahlung der blauen Tiere durch den unter den roten Tieren auf dem Spiegel liegenden Linienfokus zum Betrachter gelangt, Die beiden Zylinderlinsenhälften sind hierzu konfokal aufgestellt.

Zylinderlinsen haben in zwei senkrecht zueinander stehenden Richtungen verschiedene Krümmungen. Im engeren Sinn sind Zylinderlinsen tatsächlich Abschnitte eines Zylinders. Zylinderlinsen bzw. Linsen mit einer Zylinderkomponente werden u. a. in folgenden Fällen eingesetzt:

• Brillengläser, die Zylinderfehler der Augenlinse ausgleichen
• Breitwand-Kinoprojektoren und -Filmkameras enthalten eine Zylinderlinse, um das Bild bei Breitwandformat platzsparend auf das normale Bildformat des Kinofilms abzubilden und bei der Projektion wieder zu entzerren (Anamorphot)(Cinemascope, Totalvision und ähnliche)
• Kollimation der Strahlung von Laserdioden, die aufgrund ihres Aufbaus eine nicht kreissymetrische Divergenz besitzen.

Eine reine Zylinderlinse bündelt parallel einfallendes Licht auf eine Brennlinie.

Elastische Linsen

Der Begriff „Elastische Linse“ bezeichnet ein optisches Element, das seine Brechkraft durch die Verformung eines elastischen Festkörpers ändert. Es ergeben sich aus dem Funktionsprinzip folgende Vorteile:

• Die Form der Grenzfläche ist frei wählbar (sphärisch, asphärisch)
• Die Größe der Brechkraftänderung ist bei Verwendung von Gummimaterialien sehr groß (ca. 15 dpt)
• Die Geschwindigkeit der Verformung kann sehr schnell erfolgen

Linsenform und Brennweite

Die Lichtstrahlen werden zweimal gebrochen und konvergieren annähernd am Fokus (Abbildungsfehler)

Gleichungen für dicke Linsen

Die optischen Eigenschaften einer Linse kann man durch ihre Brennweite, mit f abgekürzt, beschreiben. Die Brennweite f ist der kürzeste Abstand zwischen der Mittelebene der Linse und dem Punkt, zu dem parallel zur optischen Achse einfallendes Licht gebündelt wird (Sammellinse) oder von dem parallel zur optischen Achse einfallendes Licht zu stammen scheint (Zerstreulinse).

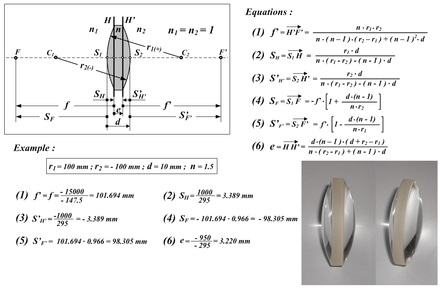
Die Brennweite hängt von den Krümmungsradien, R₁ und R₂ der beiden Linsenflächen ab. Diese können mit verschiedenen Methoden experimentell ermittelt werden. Optische Methoden sind z. B. das Autokollimationsverfahren oder die Methode von Kohlrausch. Eine mechanische Bestimmung des Krümmungsradius ist beispielsweise mit dem Ringsphärometer möglich. Mit den ermittelten Radien gilt dann für die Brennweite:

$\frac{1}{f} = \frac{n_2-n_1}{n_1} \left( \frac{1}{R_1} - \frac{1}{R_2} \right) + \frac{(n_2-n_1)^2d}{n_1 n_2 R_1 R_2}$,

wobei n₂ der Brechungsindex des Linsenmaterials, n₁ die Brechungsindex des umgebenden Mediums (z. B Luft mit n₁ = 1) und d die Dicke der Linse in ihrem Achsmittelpunkt ist. Wenn die betrachteten Linsen relativ dünn sind, kann man obige Gleichung zu

$\frac{1}{f} = \frac{n_2-n_1}{n_1} \left( \frac{1}{R_1} - \frac{1}{R_2} \right)$.

vereinfachen. Der Wert von f ist positiv für Sammellinsen und negativ für Zerstreulinsen. Der Kehrwert der Brennweite entspricht der Vergenz eines kollimierten Strahls und wird auch als Brechwert (in älteren Texten meist Brechkraft, umgangssprachlich auch Stärke) der Linse bezeichnet und in Dioptrien (1 dpt = 1/m) gemessen. Linsen, die auf einer Seite konkav, auf der anderen Seite konvex sind, und deren Krümmungsradien beider Flächen gleich sind, haben einen Brechwert von Null oder eine „unendliche“ Brennweite.

Eine wichtige Eigenschaft einer Linse ist das Prinzip von der Umkehrung des Lichtweges: Wenn ein von einer Seite einfallender Lichtstrahl entlang seines Weges verfolgt wird, so wird ein entgegengesetzt einfallender Lichtstrahl diesen Weg genau umgekehrt durchlaufen.

Die ABCD-Matrix einer (dünnen) Linse ist $L = \begin{bmatrix} 1 & 0 \\ -\frac {1}{f} & 1 \end{bmatrix}$.

Linsensysteme

Optische Systeme (Mikroskope, Fernrohre, Objektive) enthalten mehrere Linsen. Um Abbildungsfehler zu vermindern werden häufig auch theoretisch als Einzellinsen denkbare Komponenten aus mehreren Linsen zusammengesetzt. Für zwei einander berührende Linsen, die an den Berührflächen die gleiche Krümmung besitzen, lässt sich die gesamte Brennweite F, genannt Gaußsche Brennweite, aus der Brennweite der einzelnen Linsen f₁ und f₂ mittels

$\frac{1}{F} = \frac{1}{f_1} + \frac{1}{f_2} -\frac{d}{f_1f_2}$

• d = Abstand der Linsen

bestimmen, wobei d meist vernachlässigt werden kann. Diese Formel gilt nur für dünne Linsen.

Oberflächenvergütung

Bei einer realen Linse wird ein Teil des Lichtes an der Oberfläche reflektiert. Durch Oberflächenvergütung kann dieser Effekt minimiert werden.

Andere Linsentypen

• Flüssiglinse
• Fourierlinse
• Fresnellinse: Dient dem parallelen Ausrichten eines Lichtstrahls, etwa im Tageslichtprojektor oder im Leuchtturm. Auch Scheinwerfer nutzen ihr Prinzip. Auch Lupen können als Fresnellinse ausgeführt werden.
• Gaslinse: die durch die Dichte beeinflusste optische Dichte von Gasen wird genutzt, um hochenergetische Laserstrahlung zu fokussieren. Hierzu wird das Licht durch ein rotierendes Rohr geleitet, in dem das mitbewegte Gas aufgrund des Bernoulli-Effekts Linseneigenschaften annimmt.
• Gravitationslinse: Kann durch ein massereiches astronomisches Objekt wie etwa ein Schwarzes Loch gebildet werden. Vereinzelt werden dadurch ferne Galaxien als Kreisbögen oder in mehrere Punkte verzerrt.
• Diffraktive optische Elemente (DO-Glieder) werden vereinzelt in Objektiven für Spiegelreflexkameras eingesetzt.

Aufgrund der Wellennatur der Materie kann man auch mit Teilchen Optik betreiben. Eine Anwendung geschieht im Elektronenmikroskop, wo speziell angeordnete elektrische Felder und magnetische Felder Elektronen fokussieren und ablenken. Das Gleiche geschieht auch in Teilchenbeschleunigern in der Kern- und Hochenergiephysik.

Anhang

Literatur

• Heinz Haferkorn: Optik. 4. Auflage, WILEY-VCH Verlag, Weinheim 2003 ISBN 3-527-40372-8
• Miles V. Klein, Thomas E. Furtak: Optik, Springer Verlag, Berlin 1988 ISBN 3-540-18911-4
• Wolfgang Demtröder: Experimentalphysik 2 – Elektrizität und Optik, 2. Auflage, Springer-Verlag, Berlin 2002 ISBN 3-540-65196-9

Weblinks

 Commons: Linse – Album mit Bildern und/oder Videos und Audiodateien

• Brillenglas-Kompendium Umfassende Infos zu Brillenglas-Grundlagen
• www.wissenschaft.de: Erst abdrücken, dann scharfstellen – Mikrolinsen ermöglichen scharfe Bilder ohne vorheriges Fokussieren
• Linsentypen, deren Eigenschaften und Anwendungsbeispiele – Gute Gesamtübersicht mit kurzer Erläuterung zu Abbildungsfehlern (PDF-Datei; 183 kB)
• Fachstelle der Wasser und Schifffahrtsverwaltung für Verkehrstechniken Linsen und Optiken für Leuchtfeuer
• Uni Basel, imaging & media lab: Skript – Optik und Kamera (ideale Linse Teil 3 und Teil 4)
• Interaktive Simulation einer optischen Bank (benötigt Java)

Siehe auch

• Spiegel
• Linsengleichung
• Dünne Linse