k-Means-Algorithmus

Ein k-Means-Algorithmus ist ein Verfahren zur Clusteranalyse. Dabei wird aus einer Menge von ähnlichen Objekten eine vorher bekannte Anzahl von k Gruppen gebildet. Der Algorithmus ist eine der am häufigsten verwendeten Techniken zur Gruppierung von Objekten, da er schnell die Zentren der Cluster findet. Der Algorithmus hat starke Ähnlichkeiten mit dem Expectation-Maximization- und mit dem Mean-Shift-Algorithmus und zeichnet sich durch seine Einfachheit aus.^[1] Erweiterungen sind der k-Median-Algorithmus und der k-Means++ Algorithmus.

Algorithmus

Vor der Ausführung eines k-Means-Algorithmus muss die Anzahl k der zu ermittelnden Gruppen festgelegt werden.

1. Die k Cluster-Schwerpunkte werden zufällig verteilt.
2. Jedes Objekt wird demjenigen Cluster zugeordnet, dessen Schwerpunkt ihm am nächsten liegt. Dazu muss eine Distanzfunktion, zum Beispiel die euklidische Norm oder die Mahalanobis-Distanz bei nicht gleichdimensionalen Daten, verwendet werden.
3. Für jeden Cluster wird der Schwerpunkt neu berechnet, sodass dieser in der Mitte des Clusters liegt.
4. Basierend auf den neu berechneten Zentren werden die Objekte wieder wie in Schritt 2 auf die Cluster verteilt, bis

   • eine festgelegte maximale Iterationstiefe erreicht wurde oder
   • sich die Schwerpunkte nicht mehr bewegen, d. h. bei der Neuverteilung kein Objekt einem anderen Cluster zugeordnet wurde.

Lloyd-Algorithmus

Der am häufigsten verwendete k-Means-Algorithmus ist der Lloyd-Algorithmus, der manchmal auch Voronoi-Iteration genannt wird. Unter Verwendung der Methode der kleinsten Quadrate teilt er die Datenpunkte $\mathbf x_1, \mathbf x_2, \ldots, \mathbf x_n$ in k disjunkte Teilmengen S_i auf. Der Lloyd-Algorithmus versucht dabei, ein globales Minimum der Funktion

$J = \sum_{i=1}^{k} \sum_{\mathbf x_j \in S_{i}} {\| \mathbf x_j - \boldsymbol \mu_i \|^2}$

mit den Datenpunkten $\mathbf x_j$ und den Schwerpunkten $\boldsymbol \mu_i$ der Cluster S_i zu finden. Meistens kann J jedoch kaum als lokales Minimum bezeichnet werden.^[2]

Zur Durchführung werden drei Schritte abgearbeitet:

Initialisierung: Setze k zufällige Mittelwerte (Means): $\mathbf m_1^{(1)}, \ldots, \mathbf m_k^{(1)}$

Zuweisung: Jedes Datum wird dem nächsten Cluster zugewiesen.

$S_i^{(t)} = \left\{ \mathbf x_j : \big\| \mathbf x_j - \mathbf m^{(t)}_i \big\| \leq \big\| \mathbf x_j - \mathbf m^{(t)}_{i^*} \big\| \text{ fuer alle }i^*=1,\ldots,k \right\}$

Update: Berechne neue Mittelpunkte für die gebildeten Cluster:

$\mathbf m_i^{(t+1)} = \frac{1}{|S_i^{(t)}|} \sum_{\mathbf x_j \in S_{i}^{(t)}} \mathbf x_j$

Der Algorithmus wird so lange wiederholt, bis sich die Zuweisungen nicht mehr ändern.

Variationen

• k-Means ++ versucht bessere Startpunkte zu finden.^[3]
• Der Filtering-Algorithmus verwendet als Datenstruktur einen k-d-Baum.^[4]
• Der k-Means-Algorithmus kann beschleunigt werden unter Berücksichtigung der Dreiecksungleichung.^[5]

Voraussetzungen

k-Means benötigt eine Distanzfunktion und eine Funktion, die den Mittelwert berechnet. Es kann daher nur mit numerischen Attributen (inkl. binären Attributen) verwendet werden. Kategorielle Attribute (bspw. "Auto", "LKW", "Fahrrad") können nicht verwendet werden, da hier kein Mittelwert berechnet werden kann.

Der Parameter k, die Anzahl der Cluster, muss im Vorneherein bekannt sein. Er kann jedoch auch experimentell bestimmt werden, indem man verschiedene k probiert und die Ergebnisse beispielsweise mit dem Silhouettenkoeffizienten vergleicht.

Die Cluster im Datensatz müssen etwa gleich groß sein, da der Algorithmus stets an der Mitte zwischen zwei Clusterzentren den Datensatz partitioniert.

Der Datensatz darf nicht viel Rauschen / nicht viele Ausreißer enthalten. Fehlerhafte Datenobjekte verschieben die berechneten Clusterzentren oft erheblich, und der Algorithmus hat keine Vorkehrungen gegen derartige Effekte (vgl. DBSCAN, das "Noise"-Objekte explizit vorsieht).

Probleme

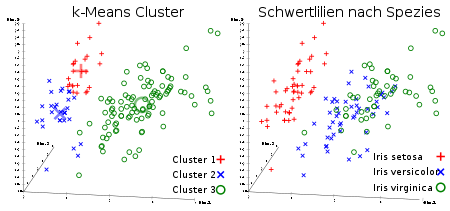k-Means Ergebnis und reale Schwertlilien-Spezies im Iris Flower Datensatz, visualisiert mit ELKI. Die Clusterzentren sind durch größere, blassere Symbole gekennzeichnet.

k-Means ist ein rechnerisch effektiver Algorithmus, es gibt jedoch auch Probleme. Ein k-Means-Algorithmus muss nicht die beste mögliche Lösung finden, jedoch ist garantiert, dass der Algorithmus eine Lösung findet. Die jeweilige Lösung hängt stark von den gewählten Startpunkten ab. Des Weiteren muss die Anzahl der Clusterzentren k im Voraus bekannt sein. Bei Verwendung eines anderen k können sich komplett andere, unter Umständen unintuitive Lösungen ergeben. Um diese Probleme zu umgehen muss die Varianz minimiert werden ohne die Komplexität zu steigern.^[6] Dies kann entweder durch die Wiederholung des Algorithmus mit verschiedenen Startpunkten erfolgen, bis die Varianz der Daten am kleinsten ist. Eine andere Möglichkeit ist es, k sukzessiv zu erhöhen. Dadurch wird die totale Varianz der Daten schnell zurückgehen. Wenn der Rückgang stagniert, ist ein guter Wert für k erreicht.

Gruppen in den Daten können sich, wie in dem gezeigten Schwertlilien-Beispiel, überlappen und nahtlos ineinander übergehen. In einem solchen Fall kann k-Means diese Gruppen nicht zuverlässig trennen, da die Daten nicht dem verwendeten Cluster-Modell folgen.

Des Weiteren sucht k-Means stets sphärische Cluster (bedingt durch die Minimierung des Abstandes zum Clustermittelpunkt). Andere Algorithmen wie DBSCAN können auch beliebig geformte „dichtebasierte“ Cluster finden. Was ebenfalls von k-Means nicht unterstützt wird, sind hierarchische Cluster (also Cluster, die wiederum eine Clusterstruktur aufweisen), wie sie beispielsweise mit OPTICS gefunden werden können.

Erweiterungen

k-Median

Im k-Median-Algorithmus wird im Zuweisungschritt statt der euklidischen Distanz die Manhattan-Distanz verwendet. Im Updateschritt wird der Median statt dem Mittelwert verwendet.^[7][8]

k-Means++

Bei dem k-Means++ Algorithmus werden die Cluster-Schwerpunkte nicht zufällig gewählt, sondern nach folgender Vorschrift:

1. Wähle als ersten Cluster-Schwerpunkt zufällig ein Objekt aus
2. Für jedes Objekt berechne den Abstand D(x) zum nächsten Cluster-Schwerpunkt
3. Wähle zufällig als nächsten Cluster-Schwerpunkt ein Objekt aus. Die Wahrscheinlichkeit mit der ein Objekt ausgewählt wird, ist proportional zu D²(x), d.h. je weiter das Objekt von den bereits gewählten Cluster-Schwerpunkten entfernt ist desto wahrscheinlicher ist es, dass es ausgewählt wird.
4. Wiederhole Schritt 2 und 3 bis k Cluster-Schwerpunkte bestimmt sind
5. Führe nun den üblichen k-Means Algorithmus aus

In der Regel konvergiert der nachfolgende k-Means Algorithmus in wenigen Schritten. Die Ergebnisse sind so gut sind wie bei einem üblichen k-Means-Algorithmus, jedoch ist der Algorithmus typischerweise fast doppelt so schnell wie der k-Means-Algorithmus.^[9]

Beispiel

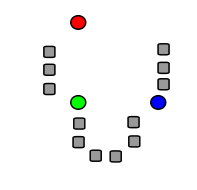
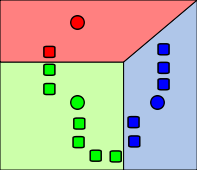
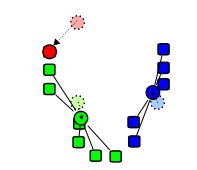
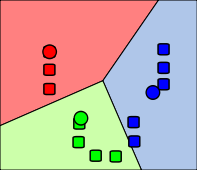
Die folgenden Bilder zeigen exemplarisch einen Durchlauf eines k-Means-Algorithmus zur Bestimmung von drei Gruppen:

	Drei Clusterzentren wurden zufällig gewählt.
	Die durch Rechtecke repräsentierten Objekte (Datenpunkte) werden jeweils dem Cluster mit dem nächsten Clusterzentrum zugeordnet.
	Die Zentren (jeweilige Schwerpunkte) der Cluster werden neu berechnet.
	Die Objekte werden neu verteilt und erneut dem Cluster zugewiesen, dessen Zentrum am nächsten ist.

Anwendung in der Bildverarbeitung

In der Bildverarbeitung wird der k-Means-Algorithmus oft zur Segmentierung verwendet. Als Entfernungsmaß ist die euklidische Distanz häufig nicht ausreichend und es können andere Abstandsfunktionen, basierend auf Pixelintensitäten und Pixelkoordinaten verwendet werden. Die Ergebnisse werden zur Trennung von Vordergrund und Hintergrund und zur Objekterkennung benutzt. Der Algorithmus ist weit verbreitet und ist in gängigen Bildverarbeitungsbibliotheken wie OpenCV und itk implementiert.

Literatur

• David MacKay: Information Theory, Inference and Learning Algorithms. Cambridge University Press, 2003, ISBN 0-521-64298-1, Chapter 20. An Example Inference Task: Clustering PDF, S. 284–292 (inference.phy.cam.ac.uk).
• Gary Bradski, Adrian Kaehler: Learning OpenCV Computer Vision with the OpenCV Library. O’Reilly, 2001, ISBN 978-0-596-51613-0.

Weblinks

• YAK-Means – Visualisierung des k-Means-Algorithmus (Java Applet)
• dei.polimi.it – Interaktives Demo des k-Means (Java Applet)

Einzelnachweise

1. ↑ Gary Bradski, Adrian Kaehler: Learning OpenCV Computer Vision with the OpenCV Library. O’Reilly, 2001, ISBN 978-0-596-51613-0, S. 479.
2. ↑ k-Means Clustering Algorithm
3. ↑ D. Arthur, S. Vassilvitskii: Slides for presentation of method (PDF)
4. ↑ T. Kanungo, D. M. Mount, N. S. Netanyahu, C. D. Piatko, R. Silverman, A. Y. Wu: An efficient k-means clustering algorithm: Analysis and implementation. In: IEEE Trans. Pattern Analysis and Machine Intelligence. 24, 2002, S. 881–892. doi:10.1109/TPAMI.2002.1017616. Abgerufen am 24. April 2009.
5. ↑ C. Elkan: Using the triangle inequality to accelerate k-means. In: Proceedings of the Twentieth International Conference on Machine Learning (ICML). 2003 (PDF).
6. ↑ Gary Bradski, Adrian Kaehler: Learning OpenCV Computer Vision with the OpenCV Library. O’Reilly, 2001, ISBN 978-0-596-51613-0, S. 480.
7. ↑ A. K. Jain and R. C. Dubes, Algorithms for Clustering Data: Prentice-Hall, 1981.
8. ↑ P. S. Bradley, O. L. Mangasarian, and W. N. Street, "Clustering via Concave Minimization," in Advances in Neural Information Processing Systems, vol. 9, M. C. Mozer, M. I. Jordan, and T. Petsche, Eds. Cambridge, MA: MIT Press, 1997, pp. 368–374.
9. ↑ T. Kanungo, D. Mount, N. Netanyahux, C. Piatko, R. Silverman, A. Wu "A Local Search Approximation Algorithm for k-Means Clustering" 2004 Computational Geometry: Theory and Applications.