Carmichaelzahl

Eine Carmichael-Zahl, benannt nach dem Mathematiker Robert Daniel Carmichael, ist eine spezielle eulersche Pseudoprimzahl, für die gilt: Eine Carmichael-Zahl n ist pseudoprim zu allen Basen, die keine gemeinsamen Primfaktoren mit n haben. Jede Carmichael-Zahl ist das Produkt aus mindestens drei Primzahlen. 1994 bewiesen Carl Pomerance, W. R. Alford und Andrew Granville die Existenz unendlich vieler Carmichael-Zahlen.^[1]

Einleitung

Es ist einfach, eine Carmichael-Zahl als solche zu erkennen, wenn man ihre sämtlichen Teiler kennt. Dies ist dem Theorem von Alwin Korselt zu verdanken. So ist es auch einfach, eine Carmichael-Zahl zu erzeugen, zumal Algorithmen wie der nach J. Chernick existieren. Problematisch ist es aber, gerade bei großen Zahlen, zu erkennen, ob es sich bei einer Zahl um eine Carmichael-Zahl handelt. Diese Schwierigkeit haben die Carmichael-Zahlen mit den Primzahlen gemeinsam, denn entweder man führt eine Faktorisierung durch, oder man wendet den kleinen fermatschen Satz auf die Zahl an, wobei man für die Basen, die nicht auf eine Primalität weisen und die bei Primzahlen nicht vorkommen, auf Teilbarkeit testen muss.

Definition einer Carmichael-Zahl

Vorbemerkung zur Kongruenz und zum Modulo

$a \equiv b \mod c$ wird „a ist kongruent zu b modulo c“ gesprochen, und ist genau dann der Fall, wenn a − b ein ganzzahliges Vielfaches von c ist.

Definition

Eine zusammengesetzte natürliche Zahl q heißt Carmichael-Zahl, falls für alle zu q teilerfremden Zahlen a gilt:

$a^{q-1} \equiv 1\quad({\rm mod\ } q),\quad \forall a \in \mathbb{Z}_q^*$

Beispiel

561 = 3*11*17 ist die kleinste Carmichael-Zahl. Für alle Basen a, die keinen Primfaktor mit 561 gemeinsam haben, gilt:

$a^{560} \equiv 1\quad ({\rm mod\ } 561)$

561 ist durch 3, 11, 17, 33, 51 und 187 teilbar. Für diese Teiler gilt $a^{q-1} \equiv 1\quad ({\rm mod\ } q)$ nicht!

$3^{560} \equiv 375 \quad ({\rm mod\ } 561)$

$11^{560} \equiv 154 \quad ({\rm mod\ } 561)$

$17^{560} \equiv 34 \quad ({\rm mod\ } 561)$

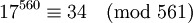
usw.

Das Theorem von Alwin Korselt

Bereits 1899 hat Alwin Korselt folgendes Theorem aufgestellt:

Es existieren ungerade, quadratfreie natürliche Zahlen n, so dass an − a für alle natürlichen Zahlen a ein Vielfaches von n ist. Für alle Primteiler p von n gilt, dass p − 1 die Zahl n − 1 teilt.

Korselt selbst hat solche Zahlen jedoch nie gefunden.

Speziell der zweite Teil des Theorems liefert eine Eigenschaft auf die Teilbarkeit der Carmichael-Zahlen:

Für eine Carmichael-Zahl c = p₁ * p₂ * p₃ * ... * p_n gilt, dass alle p_i − 1 die Zahl c − 1 teilen.

Folgerung

Aus der Tatsache, dass p_i − 1 | c − 1 kann man für alle 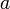$a\$ folgern, dass $a^c \equiv a \,\pmod c$

Beweis

oBdA: $p_1 \dots p_i | a$

$a^{c} \equiv 0 \equiv a \,\pmod{p_1}$

$\vdots$

$a^{c} \equiv 0 \equiv a \,\pmod{p_i}$

$a^c \equiv a^{c-1}\cdot a \equiv a^{(p_{i+1}-1) \cdot b_{i+1}} \cdot a \equiv a \,\pmod{p_{i+1}}$

$\vdots$

$a^c \equiv a^{c-1}\cdot a \equiv a^{(p_{n}-1) \cdot b_{n}} \cdot a \equiv a \,\pmod{p_{n}}$

Nach dem chinesischem Restsatz folgt nun $a^{c} \equiv a \,\pmod c$

Beispiel

Die Carmichael-Zahl 172081 ist das Produkt der Primzahlen 7, 13, 31 und 61. Es gilt:

172081 − 1 = (7 − 1) * 28680

172081 − 1 = (13 − 1) * 14340

172081 − 1 = (31 − 1) * 5736

172081 − 1 = (61 − 1) * 2868

Verschärfung

Aufgrund der Identität $n-1 = \frac{n}{p}-1+(p-1)\frac{n}{p}$ gilt für jeden Primteiler p einer natürlichen Zahl n:

$n-1\equiv\frac{n}{p}-1\pmod{p-1}$.

Somit lässt sich der zweite Teil von Korselts Satz auch formulieren als:

Eine Zahl n mit der Menge der Primteiler P ist genau dann eine Carmichael-Zahl, wenn für jedes 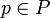$p\in P$ gilt:

p − 1 teilt $\frac{n}{p}-1$

Beispiel

Für die Carmichael-Zahl 172081 = 7 * 13 * 31 * 61 gilt:

$\frac{172081}{7} - 1 = 24583 - 1 = (7 - 1) \cdot 4097$

$\frac{172081}{13} - 1 = 13237 - 1 = (13 - 1) \cdot 1103$

$\frac{172081}{31} - 1 = 5551 - 1 = (31 - 1) \cdot 185$

$\frac{172081}{61} - 1 = 2821 - 1 = (61 - 1) \cdot 47$

Robert Daniel Carmichael

Robert Daniel Carmichael hat dann 1910 mit 561 die erste Zahl gefunden, die den Eigenschaften des Theorems von Korselt entspricht. Nach Carmichael wurden dann auch später diese Zahlen benannt.

Carmichael-Zahlen allgemein

Neben den oben aufgeführten Bedingungen für Carmichael-Zahlen von Korselt gilt für alle Carmichael-Zahlen, dass sie aus mindestens drei teilerfremden, ungeraden Primfaktoren zusammengesetzt sein müssen.

Seit 1994 weiß man, dass unendlich viele Carmichael-Zahlen existieren.

 Die ersten 36 Carmichael-Zahlen
 ---------------------------------------------------------------------------------------
   561 =  3 * 11 * 17         52633 =  7 * 73 * 103         294409 = 37 * 73 * 109
  1105 =  5 * 13 * 17         62745 =  3 *  5 *  47 *  89   314821 = 13 * 61 * 397
  1729 =  7 * 13 * 19         63973 =  7 * 13 *  19 *  37   334153 = 19 * 43 * 409
  2465 =  5 * 17 * 29         75361 = 11 * 17 *  31         340561 = 13 * 17 *  23 *  67
  2821 =  7 * 13 * 31        101101 =  7 * 11 *  13 * 101   399001 = 31 * 61 * 211
  6601 =  7 * 23 * 41        115921 = 13 * 37 * 241         410041 = 41 * 73 * 137
  8911 =  7 * 19 * 67        126217 =  7 * 13 *  19 *  73   449065 =  5 * 19 *  29 * 163
 10585 =  5 * 29 * 73        162401 = 17 * 41 * 233         488881 = 37 * 73 * 181
 15841 =  7 * 31 * 73        172081 =  7 * 13 *  31 *  61   512461 = 31 * 61 * 271
 29341 = 13 * 37 * 61        188461 =  7 * 13 *  19 * 109   530881 = 13 * 97 * 421
 41041 =  7 * 11 * 13 * 41   252601 = 41 * 61 * 101         552721 = 13 * 17 *  41 *  61
 46657 = 13 * 37 * 97        278545 =  5 * 17 *  29 * 113   656601 =  3 * 11 * 101 * 197

Carmichael-Zahlen nach J. Chernick (Carmichael-Zahl-Generator)

J. Chernick fand 1939 ein relativ einfaches System um Carmichael-Zahlen zu konstruieren:

Eine Zahl M3(m) = (6m + 1)(12m + 1)(18m + 1) ist dann eine Carmichael-Zahl, wenn alle 3 Faktoren (6m + 1), (12m + 1) und (18m + 1) Primzahlen sind.

Äquivalent dazu ist der Satz:

Sei p > 3 eine Primzahl derart, dass auch 2p-1 und 3p-2 Primzahlen sind, dann ist n = p(2p-1)(3p-2) eine Carmichael-Zahl

Unter anderem haben folgende Carmichael-Zahlen diese Struktur:

                     p       (2p-1)      (3p-2)
        M3(m)   (6m + 1)   (12m + 1)   (18m + 1)    m
---------------------------------------------------------------
        1729 =        7 *        13 *        19     1   M3(1)
      172081 =       31 *        61 *        91     5   M3(5)
      294409 =       37 *        73 *       109     6   M3(6)
     1773289 =       67 *       133 *       199    11   M3(11)
     4463641 =       91 *       181 *       271    15   M3(15)
    56052361 =      211 *       421 *       631    35   M3(35)
   118901521 =      271 *       541 *       811    45   M3(45)
   172947529 =      307 *       613 *       919    51   M3(51)
   216821881 =      331 *       661 *       991    55   M3(55)
   228842209 =      337 *       673 *      1009    56   M3(56)
  1110400109 =      557 *      1153 *      1729    96   M3(96)
  1299963601 =      601 *      1201 *      1801   100   M3(100)
  2301745249 =      727 *      1453 *      2179   121   M3(121)
  9624742921 =     1171 *      2341 *      3511   195   M3(195)
 11346205609 =     1237 *      2473 *      3709   206   M3(206)
 13079177569 =     1297 *      2593 *      3889   216   M3(216)
 21515221081 =     1531 *      3061 *      4591   255   M3(255)
 27278026129 =     1657 *      3313 *      4969   276   M3(276)
 65700513721 =     2221 *      4441 *      6661   370   M3(370)
 71171308081 =     2281 *      4561 *      6841   380   M3(380)
100264053529 =     2557 *      5113 *      7669   426   M3(426)
134642101321 =     2821 *      5641 *      8461   470   M3(470)
168003672409 =     3037 *      6073 *      9109   506   M3(506)
172018713961 =     3061 *      6121 *      9181   510   M3(510)
173032371289 =     3067 *      6133 *      9199   511   M3(511)

rote Zahlen sind Pseudoprimzahlen
grüne Zahlen sind Carmichael-Zahlen

Das Bildungsgesetz: M3(m) = (6m + 1)(12m + 1)(18m + 1) lässt sich verallgemeinern: $M_k(m) = (6m + 1)(12m + 1)\prod_{i=1}^{k-2}(9 \cdot 2^im+1)$.

Dieses Bildungsgesetz hat allerdings noch eine kleine Einschränkung: Abgesehen davon, dass alle Faktoren Primzahlen sein müssen, gilt zusätzlich, dass für (36 * 2^jm + 1) die Zahl m durch 2^j teilbar sein muss.

Die kleinste Carmichael-Zahl mit mehr als 3 Primfaktoren, die sich mit dem oben beschriebenen Bildungsgesetz bilden lässt, ist M₄(1) = 63973 = 7 * 13 * 19 * 37.

           M4(m)   (6m + 1)   (12m + 1)   (18m + 1)   (36m + 1)     m
----------------------------------------------------------------------------
          63973 =        7 *        13 *        19 *        37     1   M4(1)
   192739365541 =      271 *       541 *       811 *      1621    45   M4(45)
   461574735553 =      337 *       673 *      1009 *      2017    56   M4(56)
 10028704049893 =      727 *      1453 *      2179 *      4357   121   M4(121)
 84154807001953 =     1237 *      2473 *      3709 *      7417   206   M4(206)
197531244744661 =     1531 *      3061 *      4591 *      9181   255   M4(255) 
973694665856161 =     2281 *      4561 *      6841 *     13681   380   M4(380)

Carmichael-Zahlen nach Gerard P. Michon (Carmichael-Zahl-Generator)

Gérard P. Michon fand einen gänzlich anderen Weg, um Carmichael-Zahlen zu konstruieren:

Ein Produkt dreier Primzahlen der Form (7m+1)*(8m+1)*(11m+1) ist eine Carmichael-Zahl, wenn gilt:

• $m \equiv 326 \mod 616$
• drei teilt m (andernfalls ist mindestens einer der drei Faktoren durch 3 teilbar)
• Es existiert k mit m = 1848k + 942

Das gilt für (12936k+1)*(14784k+7537)*(20328k+10363) mit folgendem k

	m	(7m+1)	(8m+1)	(11m+1)
k	(1848k+942)	(12936k+6595)	(14784k+7537)	(20328k+10363)
13	24966	174763	199729	274627
123	228246	1597723	1825969	2510707
218	403806	2826643	3230449	4441867
223	413046	2891323	3304369	4543507
278	514686	3602803	4117489	5661547
411	760470	5323291	6083761	8365171
513	948966	6642763	7591729	10438627
551	1019190	7134331	8153521	11211091
588	1087566	7612963	8700529	11963227

Weitere k sind: 733, 743, 796, 856, 928, 1168, 1226, 1263, 1401, 1533, 1976, 1981, 2013, 2096, 2138, 2241, 2376, 2556, 2676, 2703, 3626, 3703, 3718, 3971, 4008, 4121, 4138, 4163, 4188, 4211, 4313, 4423, 4653, 4656, 4901, 5018, 5278, 5411, 5423, 5538, 5776, 5863, 5908, 6186, 6283, 6623, 6753, 6933, 7501, 7688, 7986, 8181, 8398, 8476, 8651, 8651, 8816, 8916, 8923, ...

Für k=10³²⁹-4624879 die eine 1000 stellige Carmichael-Zahl erzeugt, ergeben sich die drei folgenden Faktoren:

(12936*10³²⁹-59827428149)*(14784*10³²⁹-68374203599)*(20328*10³²⁹-94014529949)

Quellen

1. ↑ Alford, W. R.; Granville, A.; and Pomerance, C.: "There are Infinitely Many Carmichael Numbers." Ann. Math. 139 (1994), 703-722

Literatur

• Paulo Ribenboim: The New Book of Prime Number Records. Springer Verlag, 1996, ISBN 0-387-94457-5

Siehe auch

• Lucas-Carmichael-Zahl

Weblinks

• Final Answers Modular Arithmetic
• Ergänzungen und Irrtümer zu dem Buch "The new Book of Prime Number Records" von Paolo Ribenboim