- Cartesisches Blatt
-
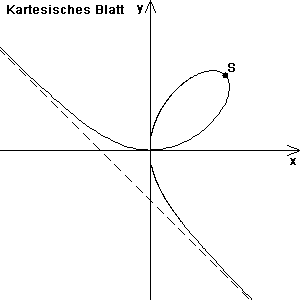
Das kartesische Blatt (oder cartesische Blatt, folium cartesii) ist eine ebene Kurve 3. Ordnung, die nach dem französischen Mathematiker und Philosophen René Descartes benannt ist.
Gleichungen des kartesischen Blattes
- Kartesische Koordinaten:
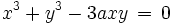
- Polarkoordinaten:
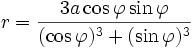
- Parametergleichung:
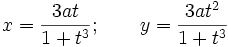
Eigenschaften des kartesischen Blattes
Im Folgenden wird jeweils vorausgesetzt, dass die Koordinatenachsen so liegen wie in der Skizze.
- Das kartesische Blatt ist achsensymmetrisch bezüglich der Winkelhalbierenden des 1. und 3. Quadranten (Gleichung y = x). Genau zwei Punkte der Kurve liegen auf der Symmetrieachse, nämlich der Ursprung und der Scheitel S mit den Koordinaten
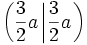 .
.
- Der Ursprung des Koordinatensystems ist ein Doppelpunkt der Kurve, d.h. er wird zweimal durchlaufen. x- und y-Achse stimmen mit den beiden Tangenten im Ursprung überein.
- Die Gerade mit der Gleichung x + y + a = 0 (in der Skizze gestrichelt) ist Asymptote der Kurve.
- Für beide Kurvenzweige beträgt der Krümmungsradius im Ursprung
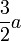 .
.
- Die Schleife des kartesischen Blattes schließt eine Fläche mit dem Inhalt
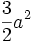 ein.
ein.
- Die Fläche, die von der Kurve und der Asymptote begrenzt wird und sich ins Unendliche erstreckt, hat denselben Flächeninhalt
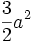 .
.
- Kartesische Koordinaten:
Wikimedia Foundation.