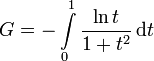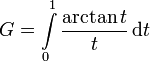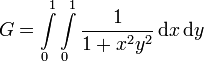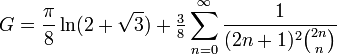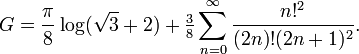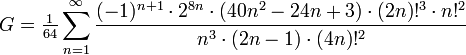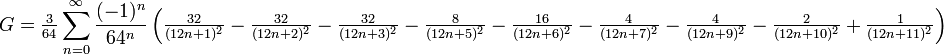Catalan-Konstante

Die catalansche Konstante, üblicherweise mit G bezeichnet, ist der Wert der Reihe

$\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)^2} = 1 - \frac1{3^2} + \frac1{5^2} - \frac1{7^2} + \cdots$,

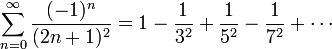also der Wert der dirichletschen Betafunktion β(2). Die Konstante ist nach Eugène Catalan (1814–1894) benannt. Ihre Irrationalität wird vermutet, ist aber bis heute unbewiesen.

Geschichte und Bezeichnung

Catalan hat diese Konstante in seiner umfangreichen Arbeit von 1883 mit G bezeichnet und zahlreiche Integral- und Reihendarstellungen dafür angegeben. Die Bezeichnung G geht vermutlich auf den Ingenieur Jacques Antoine Charles Bresse zurück.

Wert

Ein Näherunswert ist

G = 0.91596559417721901505...

Derzeit (31. Jan. 2009) sind 15.500.000.000 dezimale Nachkommastellen bekannt.^[1]

Weitere Darstellungen

Es gibt eine reichhaltige Fülle anderer Darstellungen, ein Bruchteil davon wird im Folgenden wiedergegeben:

Integraldarstellungen

$G = -\int\limits_0^1\frac{\ln t}{1 + t^2}\, {\rm d}t$

$G = \int\limits_0^1 \frac{\arctan t}{t}\, {\rm d}t$

$G = \int\limits_0^1 \int\limits_0^1 \frac{1}{1+x^2 y^2}\, {\rm d}x\,{\rm d}y$

Reihendarstellungen

Nach Ramanujan:

$G = \frac{\pi}8 \ln(2+\sqrt3) + \tfrac38 \sum_{n=0}^\infty \frac1{(2n+1)^2\binom{2n}{n}}$

und

$G = \frac{\pi}8 \log(\sqrt3 + 2) + \tfrac38 \sum_{n=0}^\infty \frac{n!^2}{(2n)!(2n+1)^2}.$

Sehr schnell konvergiert auch folgende Summe:

$G = \tfrac1{64}\sum_{n=1}^\infty \frac{(-1)^{n+1}\cdot 2^{8n}\cdot (40n^2-24n+3)\cdot (2n)!^3 \cdot n!^2}{n^3\cdot (2n-1)\cdot (4n)!^2}$

BBP-artige Reihen

Man hat lange nach einer BBP-Reihe gesucht. Zunächst wurden nur sehr lange Exemplare gefunden. Relativ kurz ist die 9-gliedrige von Victor Adamchik (2007):

$G = \tfrac3{64}\sum_{n=0}^\infty \frac{(-1)^n}{64^n}\left( \tfrac{32}{(12n+1)^2} -\tfrac{32}{(12n+2)^2} -\tfrac{32}{(12n+3)^2} -\tfrac{8}{(12n+5)^2} -\tfrac{16}{(12n+6)^2} -\tfrac{4}{(12n+7)^2} -\tfrac{4}{(12n+9)^2} -\tfrac{2}{(12n+10)^2} +\tfrac{1}{(12n+11)^2} \right)$

Quellen

• Lasar Aronowitsch Ljusternik: Mathematical Analysis. Functions, Limits, Series, Continued Fractions, 1965, S.313−314.
• Eric W. Weisstein: Catalansche Konstante auf MathWorld (englisch)

Einzelnachweise

1. ↑ http://www.numberworld.org/nagisa_runs/computations.html