Catalan-Zahl

Eugène Charles Catalan

Die Catalan-Zahlen oder catalanschen Zahlen bilden eine Folge natürlicher Zahlen, die in vielen Problemen der Kombinatorik auftritt und eine ähnlich wichtige Rolle wie die Binomialkoeffizienten oder die Fibonacci-Zahlen spielt. Sie sind nach dem belgischen Mathematiker Eugène Charles Catalan benannt.

Die Folge der Catalan-Zahlen C₀, C₁, C₂, C₃, … beginnt mit

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, … (Folge A000108 in OEIS)

Die Catalan-Zahlen sind für $n \ge 0$ gegeben durch

$C_n = \frac{1}{n+1} \binom{2n}{n} = \frac{(2n)!}{(n+1)!\,n!}\,,$

wobei $\tbinom{2n}{n}$ der mittlere Binomialkoeffizient ist. Mit $\tbinom{2n}{n+1} = \tfrac{n}{n+1} \tbinom{2n}{n}$ erhält man, dass die Formel äquivalent zu

$C_n = \binom{2n}{n} - \binom{2n}{n+1}$

ist und somit tatsächlich nur ganze Zahlen liefert.

Historisches

Die Zahlen dieser Folge wurden bereits 1751 von Leonhard Euler in einem Brief an Christian Goldbach beschrieben.^[1] Johann Andreas von Segner fand 1758 eine Rekursionsformel,^[2] zu der Euler in der Zusammenfassung zu Segners Artikel die Lösung angab.^[3] Eine von Johann Friedrich Pfaff gestellte allgemeinere Abzählungsaufgabe löste 1795 Nikolaus Fuß.^[4] In den Jahren 1838 und 1839 griffen Gabriel Lamé,^[5] Olinde Rodrigues,^[6] Jacques Binet^[7][8] und Eugène Catalan^[9][10] die Fragestellung erneut auf. Eugen Netto führte in seinem 1901 veröffentlichten Lehrbuch der Combinatorik die Zahlen auf Catalan zurück.^[11]

Eigenschaften

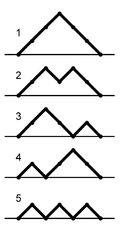
Euler suchte die Anzahl der Möglichkeiten, ein konvexes n-Eck durch Diagonalen in Dreiecke zu zerteilen (Triangulation). Diese Anzahl ist C_{n − 2}. Zum Beispiel gibt es für ein Fünfeck fünf mögliche Triangulationen:

Euler gab in dem Brief 1751^[1] die explizite Formel

$C_n = \frac{2 \cdot 6 \cdot 10 \cdots (4 n - 2)}{2 \cdot 3 \cdot 4 \cdots (n+1)} = \prod_{k=1}^n \frac{4 k - 2}{k + 1} \qquad (*)$

und die Formel

$\sum_{n=0}^\infty C_n x^n = \frac{1 - \sqrt{1 - 4 x}}{2 x} = \frac{2}{1 + \sqrt{1 - 4 x}}$

für die erzeugende Funktion an, insbesondere

$\sum_{n=0}^\infty \frac{C_n}{4^n} = 2$

auch als Beschreibung des Wachstumsverhaltens.

Direkt aus der Formel (*) folgt

$C_{n+1} = \frac{4 n + 2}{n + 2}\,C_n\,.$

Es gilt außerdem die Rekursionsformel (Segner 1758)^[2]

$C_{n+1} = \sum_{k=0}^n C_k\,C_{n-k}\,,$

zum Beispiel ist C₃ = C₀ C₂ + C₁ C₁ + C₂ C₀.

Eine weitere Rekursionsformel ist

$C_{n+1} = \sum_{k=0}^{\lfloor n/2 \rfloor} \binom{n}{2k} 2^{n-2k}\,C_k\,.$

Da alle Primfaktoren von $\textstyle C_n = 2^n\,\frac{1 \cdot 3 \cdot 5 \cdots (2n-1)}{2 \cdot 3 \cdot 4 \cdots (n+1)}$, siehe Formel (*), kleiner als 2n sind und C_n > 2n für n > 3, sind C₂ = 2 und C₃ = 5 als einzige Catalan-Zahlen auch Primzahlen. Die Formel zeigt auch, dass C_n durch jede Primzahl zwischen n + 1 und 2n genau einmal teilbar ist und genau dann ungerade, wenn n = 2^k − 1 für eine ganze Zahl k.

Aus dem Satz von Wolstenholme folgt die Kongruenz

$(p\,n + 1)\,C_{p\,n} \equiv (n + 1)\,C_n \ (\text{mod }p^3)$

für jede Primzahl p > 3, für Wolstenholme-Primzahlen gilt die Kongruenz (mod p⁴), für die Primzahlen 2 und 3 gilt sie (mod p²).

Insbesondere ist $C_{p^k n} \equiv (n + 1)\,C_n \ (\text{mod }p)$ und $C_{p^k} \equiv 2 \ (\text{mod }p)$ für jede Primzahl p und ganze Zahl k > 0.

Durch Einsetzen der Stirling-Formel erhält man für das asymptotische Verhalten der Catalan-Zahlen

$C_n \sim 4^n / \bigl((n+1) \sqrt{\pi n}\,\bigr)\,.$

Weitere Interpretationen

Die Catalan-Zahlen treten bei zahlreichen Abzählungsaufgaben, die graphentheoretisch Abzählungen von Bäumen sind, auf. So ist C_n die Anzahl der

• Beklammerungen eines Produktes, in dem n Multiplikationen vorkommen, oder, gleichbedeutend, mit n+1 Faktoren, so dass immer nur die Multiplikation von zwei Faktoren durchzuführen ist (Catalan 1838).^[9] Beispielsweise ist C₃ = 5, denn alle möglichen Beklammerungen von x₁x₂x₃x₄ sind (x₁x₂)(x₃x₄), (x₁(x₂x₃))x₄, x₁((x₂x₃)x₄), ((x₁x₂)x₃)x₄ und x₁(x₂(x₃x₄)).
• eindimensionalen Irrfahrten von 0 nach 2n mit Anfangs- und Endpunkt in 0, so dass sich der Pfad nie unterhalb der x-Achse befindet. Zum Beispiel ist C₃ = 5, denn alle möglichen Pfade sind:

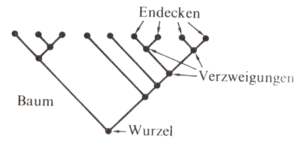
• Binärbäume mit 2n+1 Knoten oder, gleichbedeutend, mit n+1 Blättern (= Endecken). Beispiel für n=8:

Literatur

• Peter J. Hilton, Jean Pedersen: Catalan-Zahlen und Wege in einem ganzzahligen Gitter, Elemente der Mathematik 48, 1993, S. 45–60 (bei retro.seals.ch: [2])
• Jürgen Schmidthammer: Catalan-Zahlen (PDF-Datei, 7,05 MB), Zulassungsarbeit zum Staatsexamen, Erlangen Februar 1996
• Richard P. Stanley: Enumerative combinatorics Band 2, Cambridge University Press, Cambridge 1999, ISBN 0-521-56069-1 (englisch; Stanleys Webseite zum Buch mit laufend aktualisierter Liste zu Interpretationen der Catalan-Zahlen: Information on Enumerative Combinatorics)

Weblinks

 Commons: Catalan-Zahlen – Sammlung von Bildern, Videos und Audiodateien

• Eric W. Weisstein: Catalan Number. In: MathWorld. (englisch)
• Lattice Paths: Catalan Numbers in der NIST Digital Library of Mathematical Functions (englisch)

Einzelnachweise

1. ↑ ^{a b} Brief von Euler an Goldbach vom 4. September 1751 (im Euler-Archiv: [1], PDF-Datei, 137 kB)
2. ↑ ^{a b} Ioh. Andr. de Segner: Enumeratio modorum quibus figurae planae rectilineae per diagonales dividuntur in triangula, Novi commentarii academiae scientiarum imperialis petropolitanae 7 pro annis 1758 et 1759, 1761, S. 203–210 (lateinisch)
3. ↑ Leonhard Euler: Summarium dissertationum, Novi commentarii academiae scientiarum imperialis petropolitanae 7 pro annis 1758 et 1759, 1761, S. 13–15 (lateinisch)
4. ↑ Nicolao Fuss: Solutio quaestionis, quot modis polygonum n laterum in polygona m laterum, per diagonales resolvi queat, Nova acta academiae scientiarum imperialis petropolitanae 9, 1795, S. 243–251 (lateinisch)
5. ↑ Gabriel Lamé: Extrait d’une lettre de M. Lamé à M. Liouville sur cette question: Un polygone convexe étant donné, de combien de manières peut-on le partager en triangles au moyen de diagonales?, Journal de mathématiques pures et appliquées 3, 1838, S. 505–507 (französisch)
6. ↑ Olinde Rodrigues: Sur le nombre de manières de décomposer un polygone en triangles au moyen de diagonales und Sur le nombre de manières d’effectuer un produit de n facteurs, Journal de mathématiques pures et appliquées 3, 1838, S. 547–549 (französisch)
7. ↑ J. Binet: Problèmes sur les polygones, Société philomathique de Paris – Séances de 1838 – Extraits des procès-verbaux, S. 127–129 (französisch)
8. ↑ J. Binet: Réflexions sur le problème de déterminer le nombre de manières dont une figure rectiligne peut être partagée en triangles au moyen de ses diagonales, Journal de mathématiques pures et appliquées 4, 1839, S. 79–90 (französisch)
9. ↑ ^{a b} E. Catalan: Note sur une équation aux différences finies, Journal de mathématiques pures et appliquées 3, 1838, S. 508–516, und 4, 1838, S. 95–99 (französisch)
10. ↑ E. Catalan: Solution nouvelle de cette question: Un polygone étant donné, de combien de manières peut-on le partager en triangles au moyen de diagonales?, Journal de mathématiques pures et appliquées 4, 1839, S. 91–94 (französisch)
11. ↑ Eugen Netto: Lehrbuch der Combinatorik, B. G. Teubner, Leipzig 1901 (Zurückführung der Zahlen auf Catalan in § 122, S. 192–194 und § 124, S. 195)