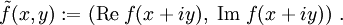Cauchy-Riemann-Gleichungen

Die Cauchy-Riemann'schen partiellen Differentialgleichungen (nach Augustin Louis Cauchy und Bernhard Riemann) sind ein Begriff aus der Funktionentheorie und ein Kriterium für komplexe Differenzierbarkeit. Die Gleichungen wurden das erste Mal 1814 von Cauchy in seinem Aufsatz Sur les intégrales définies aufgeschrieben.

Bezeichnungen

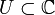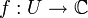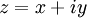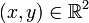Sei $U \subset \mathbb{C}$ offen und $f:U \rightarrow \mathbb{C}$ eine komplexwertige Funktion einer komplexen Variablen. In kanonischer Weise kann man eine komplexe Zahl $\ z=x+iy$ mit $(x,y) \in \mathbb{R}^2$ identifizieren. 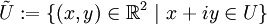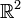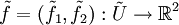Sei $\tilde{U} := \{(x,y)\in\mathbb{R}^2\ |\ x+iy \in U\}$ das entsprechende Pendant zu U im $\mathbb{R}^2$ und $\tilde{f} = (\tilde{f}_1, \tilde{f}_2): \tilde{U} \rightarrow \mathbb{R}^2$ definiert vermöge

$\tilde{f}(x,y) := ({\rm Re}\; f(x+iy),\; {\rm Im}\; f(x+iy))\ .$

Die Cauchy-Riemann'schen Differentialgleichungen klären nun den Zusammenhang zwischen der komplexen Differenzierbarkeit von f und der Differenzierbarkeit von 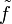$\tilde{f}$ im folgenden Sinne:

Formulierung

Es gelten die Bezeichnungen von oben; insbesondere sei darauf hingewiesen, dass U offen ist. Sei 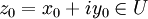$z_0 = x_0 + iy_0 \in U$. Dann sind äquivalent:

• f ist in z₀ komplex differenzierbar.
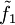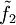• Es existieren die partiellen Ableitungen von $\tilde{f}_1$ und $\tilde{f}_2$ nach x und y die in (x₀,y₀) stetig sind, und es gelten die Cauchy-Riemann'schen Differentialgleichungen

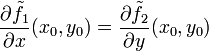$\frac{\partial \tilde{f}_1}{\partial x}(x_0, y_0) = \frac{\partial \tilde{f}_2}{\partial y}(x_0, y_0)$ und $\frac{\partial \tilde{f}_1}{\partial y}(x_0, y_0) = -\frac{\partial \tilde{f}_2}{\partial x}(x_0, y_0)$.

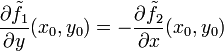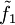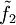Mit Hilfe der Cauchy-Riemann'schen Differentialgleichungen kann man zeigen, dass $\tilde{f}_1$ und $\tilde{f}_2$ harmonische Funktionen sind, sofern f holomorph ist.

Literatur

• Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 3. Auflage. Springer, 2000, ISBN 3540676414.